【１次関数】 時間と道のりの関係を表すグラフ
![[問題]Ａさんは、家から2400m離れた公園まで歩いた。Ａさんが家を出てから10分後に兄が自転車で家を出発し、Ａさんと同じ道を休むことなく、分速160mで公園に向かった。右の図は、Ａさんが家を出てからの時間をx分、家からの道のりをymとして、xとyの関係を表したグラフである。この問題で，兄の進行の様子を表すグラフをどうかけばいいのかわかりません。](/teikitest/_resource/img/chu/math/c_m_337_1.png)
進研ゼミからの回答
(道のり)＝(速さ)×(時間)が成り立つので，一定の速さで進む場合，(時間x)と(道のりy)の関係は1次関数になり，グラフに表すと直線になります。
座標(x, y)は，いつ(x)，どこ(y)にいるのかということを表し，一定の速さで進むので, 直線の傾きは速さを表しています。
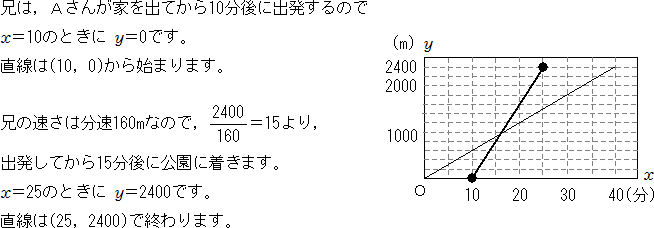
(10，0)と(25，2400)を結ぶ線分が求めるグラフです。また，このグラフの直線の式は
y＝160x-1600です。
みつかる、明日のまなび。
