【図形の性質】方べきの定理ってどういうときに出てくるんですか?
方べきの定理ってどういうときに出てくるんですか?
使い方もよくわかりません。詳しく教えてください。
進研ゼミからの回答
こんにちは。ご質問いただきありがとうございます。
【質問の確認】
「方べきの定理ってどういうときに出てくるんですか?
使い方もよくわかりません。詳しく教えてください。」とのご質問ですね。
方べきの定理について一緒に確認していきましょう。
【解説】
まずは方べきの定理を確認しておきましょう。
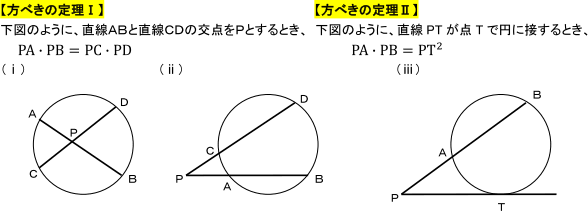
この定理が成り立つことの証明は教科書などにもあるので参考にしてみるとよいですね。
さてこれをどういうときに使うかですね。
円と2直線が交わった図の問題があれば、この「方べきの定理」を思い出して、
利用できないか考えてみましょう。以下に具体的な出題パターンを挙げてみますね。
◆まず一番基本としては、この定理を利用して線分の長さを求めることができます。
上の図にあるような図のときは機械的に、定理の式にわかっている値を代入していけば
求められますね。
ただ、少し違う図形に見えたり、求めるものが方べきの定理に現れている線分そのものではない場合になると、方べきの定理を使う問題だと気づきにくい場合があります。以下の例を参考に見てみましょう。

どこで方べきの定理を使うかイメージできましたか?

この問題のように、はじめに示した図と少し見え方が異なり、方べきの定理を使って直接求めたいものを求めることができないときでも定理を適用することを思いつけるかどうかが大切ですね。

【アドバイス】
定理だけ見ていると、何の意味があるの?と思いがちですが、まずは実際に使って慣れていくとよいですね。そこから次第に理解が深まっていくと思います。
「ゼミ」教材には、今回紹介した例題のすべてのパターンが出ているので、ぜひこの機会にあわせてやってみましょう。方べきの定理のさらなる理解につながると思いますよ。
















