【図形の性質】回転体で「内部が通過する部分」と「側面が通過する部分」の意味
「内部が通過する部分」と「側面が通過する部分」の意味がわからない。
進研ゼミからの回答
こんにちは。
では質問にお答えします。
【質問の確認】
【問題】
1辺の長さが6である正四面体ABCDにおいて,三角形BCDの重心をGとする。この正四面体を直線AGを軸にして1回転させる。ただし,線分AGは底面BCDに垂直であることを用いてよい。
(1)AGの長さを求めよ。
(2)この正四面体の内部が通過する部分の体積を求めよ。
(3)この正四面体の側面が通過する部分の体積を求めよ。
について,
(2)の「内部が通過する部分」と(3)の「側面が通過する部分」の意味がわからない。
というご質問ですね。
【解説】
≪回転軸に垂直な平面で考える≫
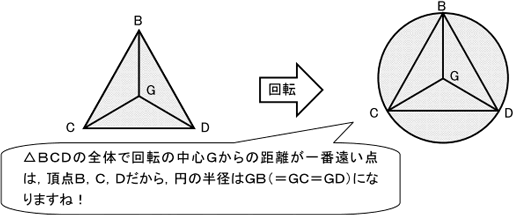
まずはわかりやすいように平面で説明します。底面の△BCDを重心G を中心に回転させたとき, (ⅰ)△BCDの内部も含む全体が通過する領域,(ⅱ)△BCDの3辺(内部は含まない)が通過する領域をそれぞれ考えてみましょう。
(ⅰ)△BCDの内部も含めた「全体」が通過する領域は重心Gを中心とする半径GBの円です!
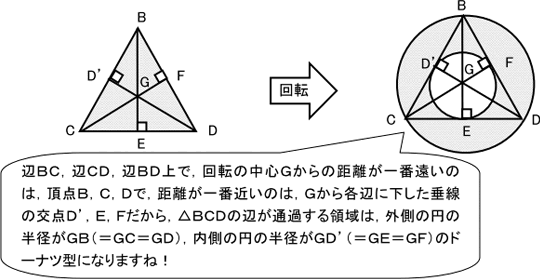
(ⅱ)△BCDの「辺BC,辺CD,辺BD」が通過する部分は,重心Gを中心とする半径GBの円と重心Gを中心とする半径GD’(=GE=GF)の円で囲まれたドーナツ型になります!
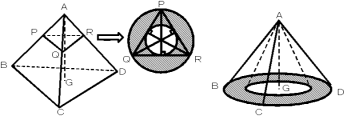
≪正四面体を回転させる場合≫
では本題に入ります。正四面体ABCDを直線AGを軸として回転させる場合を考えましょう。
(2)の「内部が通過する部分」というのは,立体の内部も含む全体の通過領域をさし,(3)の「側面が通過する部分」というのは,3つの側面△ABC,△ACD,△ADBの通過領域を示しており,この場合,正四面体の内部は含みません。平面での説明に対応させると,(2)は(ⅰ),(3)は(ⅱ)に対応しています。
正四面体ABCDを直線AGに垂直に切った断面図は,どこで切っても正三角形で,それを回転させたとき正三角形の「辺」の通過領域はドーナツ型ですね。だから,正四面体ABCDを直線AGを中心に回転させると,四面体の「側面」の通過領域は,だんだん小さくなるドーナツ型が積み重なった,「大きな円錐-小さな円錐」になる訳です。
【アドバイス】
まずは底面だけを回転させて平面で考えてみると,「内部の通過領域」,「辺(側面)の通過領域」の違いが明確になるでしょう。
またわからないことがあったら質問を送ってくださいね。













