【物質量】有効数字の考え方について
34.97×75.77/100+36.97×24.23/100=26.496769+8.957831=35.4546=35.5で,答えが35.5になったんですけど,この答えではダメですか。
進研ゼミからの回答
こんにちは。がんばっておられますね。
【質問の確認】
【問題】 天然において,塩素原子には2種類の同位体が存在する。

上の表を参考にして,塩素の原子量を有効数字3桁で求めよ。
という問題について,
【解答解説】
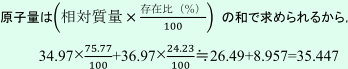
有効数字3桁で表して,35.4
の計算結果が35.5ではなく35.4となる理由について解説します。
【解説】
有効数字について確認したうえで,有効数字の計算規則に従って答えを算出していきましょう。
■有効数字とは
測定値や測定値を使った計算で得られた値は,末位に誤差を含みます。誤差を含みながらも,測定値として意味をもつ桁だけを表示したものが,有効数字です。
例)最小目盛りが1mmの,一般的な定規を考えます。
この定規であるものの長さをはかったとき,端が12mmと13mmの,ちょうど真ん中にかかったとします。このとき,長さを12mmまたは13mmとするより12.5mmとする方が,実際の長さに 近くなります。この測定結果「12.5mm」は,末位の「5」に誤差を含みながらも測定値として有効な桁だけを表示した有効数字です。
理科で扱う数値,例えば今回の計算に使う相対質量・存在比だけでなく,質量・体積・濃度・アボガドロ数や原子量その他など,大半が有効数字です。
■有効数字の桁数の数え方
次の例では,下線を引いた部分の桁数を数えます。

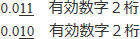
(末位の「0」も数えます)
大きい有効数字,または小さい有効数字は,一桁目と二桁目の間に小数点がくるよう指数で調整して表示します。
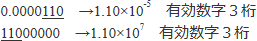
■有効数字の計算
有効数字を使った計算では,誤差が拡大したり不要な桁が増えたりしないように切り捨てを行いながら計算を進め,最終的な答えを出すときに四捨五入を行います。
今回の計算は,問題文に有効数字3桁で答えるよう指定されているため,次の規則で計算を進めます。
①途中計算は,求める答えより1桁多い4桁を残し,以下を切り捨て
②最終的な答えだけ,残しておいた4桁目を四捨五入して3桁とする
この規則に従って問題の計算を進めると,次のようになります。

残しておいた4桁目を四捨五入して有効数字3桁にすると,
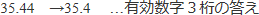
【アドバイス】
理科では常に有効数字を意識し,表示方法や桁数にも注意を払い,規則に従った計算を進めていきましょう。
ゼミ教材では規則に従って有効数字を扱っていますので,参考にしてください。












