【微分法(III)】置き換えによる微分
「 y=(2x+1)^3+(2x+1)を微分せよ。」という問題の解答を見ると,u =2x+1 とおいているのですが,どうしてこのような解き方をするのですか? このやり方がわかりません。教えてください。
進研ゼミからの回答
こんにちは。
いただいた質問について,さっそく回答いたします。
【質問の確認】
【問題】次の関数を微分せよ
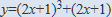
上の問題の解答を見ると,u=2x+1とおいているのですが,どうしてこのような解き方をするのですか?
というご質問ですね。
【解説】

合成関数の導関数
微分可能な2つの関数y = f(u),u = g(x) の合成関数y = f(g(x)) について,
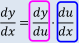
これを利用して解くと,次のようになります。
まず,

では,微分の仕方をまとめておきましょう。

≪合成関数の導関数の公式≫
合成関数は,(外側の関数を微分)×(中の小さい関数を微分)×(さらにその中の関数を微分)×……というように,外から内へドンドン微分して掛ける,と考えます。
①を例にとってみると,次のようなイメージです。
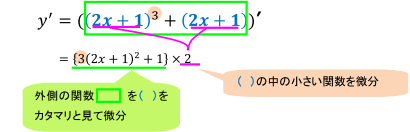
このように考えると,2x+1をu とおいてステップを3回踏まなくても,一気に微分できてしまいます。
ポイントは,
・カタマリをつくり,外側の関数と中の小さな関数をとらえる
・外側から微分する
です。
【アドバイス】
次数が高い式など,y = f(g(x)) の形をしているときは,「合成関数の導関数」の公式を確実に利用できるようにしておきましょう。まずは,u = g(x) とおいて,3ステップで確実に解けるように練習しておきましょう。
慣れてくれば,
・カタマリをつくり,外側の関数と中の小さな関数をとらえる
・外側から微分する
というポイントを押さえ一気に微分してもよいでしょう。
それでは,これで回答を終わります。
これからも,『進研ゼミ高校講座』にしっかりと取り組んでいってくださいね。
















