(受験生にオススメ)【関数と極限】はさみうちの原理の使い方について
解答では
x→0の時のh^(p-1)sin1/hを,0≦|sin1/h|≦1より…というように絶対値をつけて求めていますが
つける理由がわかりません。
また(2)の解答を見るとp=2のとき、
f(x)はx=0で微分可能である
f’(x)はx=0のとき連続ではない
と読み取りました。
「微分可能であれば連続である」と習ったので混乱しています。もしかすると特別な関係なのでしょうか。
進研ゼミからの回答
こんにちは。
では、いただいた質問について、回答します。
【質問内容】
【問題】

【解答解説】から抜粋部分
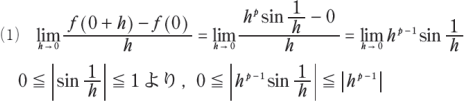
2行目からはどうして勝手に絶対値をつけるのかという質問と、

(2)の解答で、
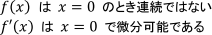
と読み取れましたが、「微分可能であれば連続である」と習ったので混乱しています。もしかすると特別な関係なのでしょうか。
という質問ですね。
【質問への回答】
《絶対値の質問について》
ついていなくてもよい記号をなぜつけるのか、という疑問でしょうか。
確かに、絶対値記号を使わなくてもはさめるので、極限値を求めることはできます。
もし絶対値を利用しないと、このような回答になります。
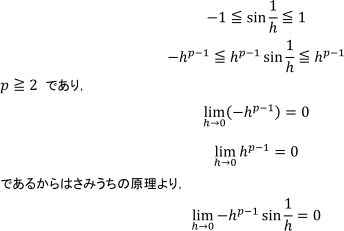
本解と見比べてわかったと思います。解答が冗長になるのを避けるためのテクニックだったのです。
《p=2のときについて》
あなたがおっしゃるように、p=2の場合は

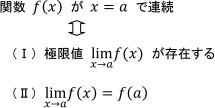
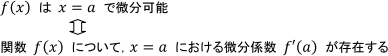

【学習アドバイス】
この問題の目的は、関数がなんであれ、定義に従って、連続や微分可能性を調べる力です。
グラフを想像して、曲線が滑らかなイメージ(微分可能)、つながっているイメージ(連続)と、結びつけたいところですが、あえて、安易にそうできないような関数で、鍛えているわけですね。
とはいえ、今回の質問から、あなたがよく考え、よりいっそう理解しようとされていることがわかります。
この調子で、がんばってください。
応援しています。
















