関数と極限|逆関数の意味|数学Ⅲ|定期テスト対策サイト

数学Ⅲ 定期テスト対策【関数と極限】逆関数の意味

【関数と極限】逆関数の意味

逆関数では，xとyを入れかえますが，何のために入れかえるのかわかりません。逆関数の意味を教えてください。

進研ゼミからの回答

こんにちは。
いただいた質問について，さっそく回答いたします。

【質問の確認】

逆関数では，xとyを入れかえますが，何のために入れかえるのかわかりません。逆関数の意味を教えてください。
というご質問ですね。

【解説】

逆関数では，xとyを入れかえる操作をしますが，それはなぜでしょう・・・。
ここで，あらためて逆関数の意味をしっかり理解していきましょう。

≪逆関数の定義≫
まず，関数の意味を確認しておきましょう。

２つの変数x， yについて，xの値を決めるとそれに応じてyの値がただ１つ定まるとき，y は x の関数であるという。

例えば，関数 f(x)=2x+3 は，xの値を１つ決めると，それに応じてyの値が１つ決まります。

$【解説】01$

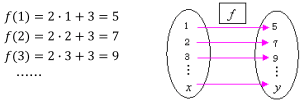
この関数を言葉で表すと，「ある数を２倍して，それから３を加えた数をつくる関数」です。

逆関数とは，xとyの「役割」を交換し，同じ対応を逆から見た関数のことです。

$【解説】02$
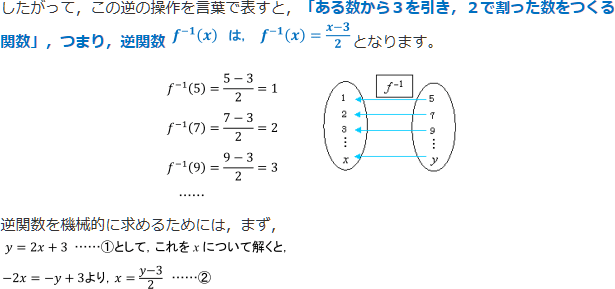
ここで，数学のルールでは，一般に，関数を「xの関数」で表すので，②の式でもこのルールにそろえます。つまり，②の式において，xをyに，yをxに書きかえます。（このことを，「xとyを入れかえる」と表現しています。）

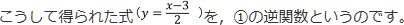
$【解説】逆関数の意味$

では，関数 y=f(x) の逆関数 y=g(x) を求めるときの手順をまとめておきましょう。

【逆関数の求め方】
[Step 1]　y = f(x) という関係式を，独立変数xについて解き， x = g(y) の形にする。

[Step 2]　独立変数が x，従属変数が y になるように書きかえて(つまり，多くの場合，x を y に，y を x に書きかえて)， y= g(x)とする。

また，逆関数の定義より，逆関数は次の性質を持ちます。

【逆関数の性質】
（１）逆関数では，もとの関数の定義域，値域が，値域，定義域となる。
（２）y = f(x) のグラフとその逆関数 y=g(x) のグラフは，直線 y=x に関して対称である。

この性質を生かして，関数 y=f(x) のグラフの形がわかりにくいとき，逆関数 y=g(x) のグラフを利用して，もとの関数のグラフの概形をつかむということもあります。しっかり理解しておきましょう。