【複素数平面】複素数の極形式
解答の途中式で,なぜ-cosθ-i sinθ=cos(θ+π)+i sin(θ+π)になるのかがわかりません。
進研ゼミからの回答
こんにちは。頑張って数学の学習に取り組めていますね。
いただいた質問について、早速回答いたします。
【質問内容】
【問題】
次の複素数を極形式で表せ。
-3(cosθ+isinθ)
【解答解説】から抜粋部分
極形式ではr>0であるから、
-3(cosθ+isinθ)=3(-cosθ-isinθ)
=3{cos(θ+π)+isin(θ+π)}
ゆえに、
-3(cosθ+isinθ)=3{cos(θ+π)+isin(θ+π)}・・・・・・(答)
解答の途中式でなぜ-cosθ-isinθ=cos(θ+π)+isin(θ+π)になるのかがわかりません。
というご質問ですね。
【質問への解答】
まず、-3(cosθ+isinθ)を変形して、
-3(cosθ+isinθ)=3(-cosθ-isinθ)・・・★
となることは大丈夫でしょうか?
極形式 r(cosθ+isinθ)では、r>0としなくてはいけないから、まずこの変形をします。
さらに次の【(θ+π)の三角関数】を利用して変形していきます。
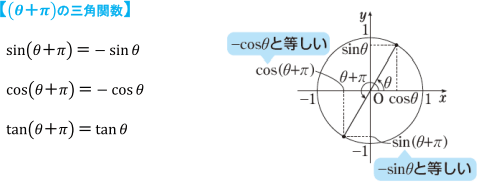
つまり上の★の式に、-cosθ=cos(θ+π),-sinθ=sin(θ+π)を代入すれば、
-3(cosθ+isinθ)=3(-cosθ-isinθ)
=3{-cosθ+i×(-sinθ)}
=3{cos(θ+π)+isin(θ+π)}
と式変形できます。
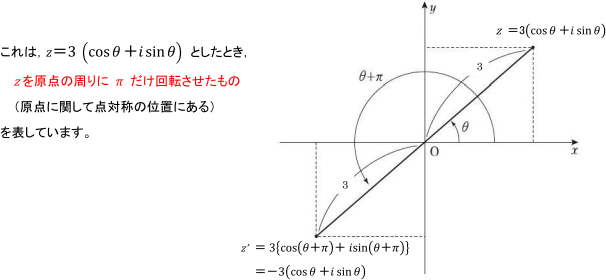
この問題は、-3(cosθ+isinθ) を r(cosθ+isinθ)という極形式に直す問題ですね。
極形式で表すには、その複素数を a+bi と表したとき、複素数平面上にその点をとってみるとよいでしょう。

Pを原点Oに関して対称移動した点Qは、-3cosθ+(-3sinθ)i となります。
したがって、点Qの動径はr=3、偏角はθ+πとなるので、
-3cosθ+(-3sinθ)i=3{cos(θ+π)+isin(θ+π)}
と極形式で表せることになります。
【学習アドバイス】
複素数zの極形式z=r(cosθ+isinθ)において、
-zはzを原点のまわりにπだけ回転させた点である。
と考えることができます。
r=|Z|(zの絶対値)だから、r>0 となります。そこで、r>0として式変形できるように練習しましょう。
また、極形式に直すときは、複素数平面に a+bi を表す点(a,b)をとってみましょう。すると、原点からの距離rと偏角が見えてきますよ。
では、これからも『進研ゼミ高校講座』にしっかりと取り組んでいってくださいね。
















