【指数・対数関数】対数の性質が成り立つ理由
対数の性質3.について,なぜそういう風になるのかがわかりません。
進研ゼミからの回答
質問をいただいたのでお答えします。
【質問の確認】

について,性質3.がなぜ成り立つのかわかりません。
というご質問ですね。
【解説】
まず,次の「対数の定義」はOKでしょうか?
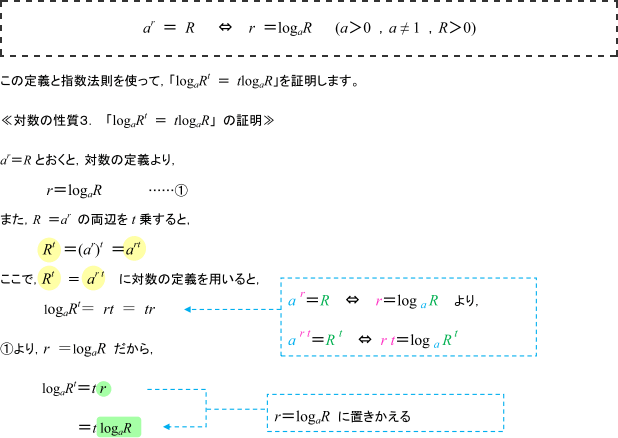
このように証明できます。
定義をきちんと押さえて,指数の関係を対数の関係に,または,対数の関係を指数の関係に直すことがポイントになります。これらに慣れることで,対数関数の力がグーンとついてきますよ。
例えば,t=3,t=-3のように,t が整数の場合は,性質1.2.から次のように導くこともできます。
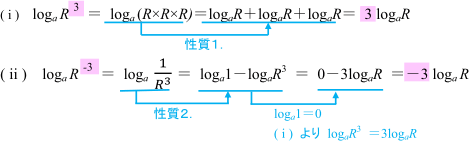
【アドバイス】
対数関数は最初はなかなかなじみにくいと思いますが,
「対数の定義」(指数関数と対数関数の関係)
をしっかりとつかみ,これをもとにして対数の性質を考えていくことがポイントです。
対数の性質を自分で証明できるようにしておくと,その性質の意味が理解できて忘れにくくなりますから,証明を確認し,自分でできるようにしておきましょう。
では,この調子でがんばって『進研ゼミ高校講座』を活用して,実戦力を養っていってくださいね。
応援しています。
















