【関数と極限】数列の極限について
数列の極限を求めるのに,値を代入して∞/∞ や0/0 となったから1,∞-∞となったから0としたら答えが違っていました。
進研ゼミからの回答
こんにちは。
いただいた質問について,さっそく回答いたします。
【質問の確認】
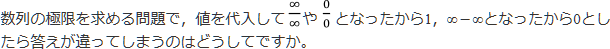
というご質問ですね。
【解説】
極限を求める式は,例えば,
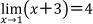
と書きますが,xは1という値そのものになるのではなく,あくまでも,xを1に限りなく近づけたら,x+3は4に限りなく近づく,つまり,
x →1のとき,x+3 →4
という状況を考えています。
また,∞は,限りなく大きいことを表す記号であって,限りなく大きな数値ではありません。x →∞は,変数xが限りなく大きくなる状況を表しているのです。
つまり,極限を求めるときは状況を考えてみるとよいということです。これを踏まえて,次のようなステップで極限を求めてみましょう。
≪Step 1 変数が限りなく大きくなると,どんな状況になるかを確認する≫

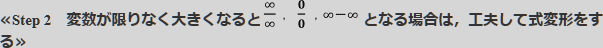

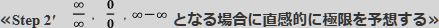

≪Step 3 直接極限がわかる形に式変形できないときは,はさみうちの原理を利用する≫
まず,はさみうちの原理を確認しておきましょう。

◎まとめ
極限を求めるときは,上の3つのStepを考えましょう。

【アドバイス】

それでは,これで回答を終わります。
これからも,『進研ゼミ高校講座』にしっかりと取り組んでいってくださいね。