【平面上の曲線】媒介変数表示について
座標平面上における直線や曲線は,xとyの関係式で表すのに,「媒介変数表示」はxとyのほかに,別の文字が入っていて,どう扱えばよいのかわかりません。
進研ゼミからの回答
こんにちは。
いただいた質問について,さっそく回答いたします。
【質問の確認】
座標平面上における直線や曲線は,xとyの関係式で表すのに,「媒介変数表示」ではxとyのほかに,別の文字が入っていて,どう扱えばよいのかわかりません。
というご質問ですね。
【解説】
≪「媒介変数表示」の意味≫
「媒介変数表示」というと,なんだか難しそうな言葉ですが,「媒介」とは,双方の間に立ってとりもつことですから,要は x と y は変数tを媒介にしてつながっている,ということです。
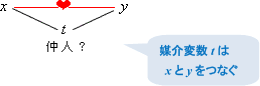
例えば,時間とともに動く点P(x,y) の座標が時刻 tによって,
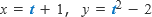
と表されているとします。このとき,時刻tの値が1つ決まれば,点Pの座標が1つ決まります。この t が媒介変数であり,x と y は媒介変数表示されている,というわけです。

もちろん,この例のように時刻でなくても,2つの変数(x と y)をとりもっていれば媒介変数ですから,媒介変数は t とは限らず,θや u などいろいろな変数の場合があります。
≪媒介変数表示された関数の扱い方≫
具体例で説明しましょう。
普通,座標平面上における直線や曲線は,x と y の関係式で表しましたね。そこで,x と y の関係が知りたいならば,t には消えてもらえばよいのです。

xもyもtの式で表されています。つまり,xとyの間をとりもつ媒介変数tを用いた表し方ということですね。
これがどのような図形を表すかを調べるためには,tを消去して,xとyの関係式を求めればいいのです。
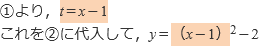
この式は,おなじみの2次関数の式ですね。
よって,この図形は点( 1,-2)を頂点とする放物線になることがわかります。

よって,この図形は中心( 2,-1 ) ,半径1の円になることがわかります。
◎まとめ
媒介変数表示とは,直線や曲線の表し方の1つですから,xとyの関係や,どのような図形かを調べるためには, 媒介変数を消去して,xとyの関係式にすればよいのです。
ただし,もし媒介変数の値の範囲が限られている場合は,x,yの値の範囲にも気をつけなければなりません。
例えば,【例1】で t≧0という条件があったなら,
t=x-1≧0より,x≧1
となり,この図形は点( 1,-2 ) を頂点とする放物線のx≧1の部分ということになるわけです。
【アドバイス】
媒介変数表示で,xとyの関係を求めたいときは,“媒介変数を消去する”ことを覚えておいてください。消去の仕方は【例1】のように簡単なものや【例2】のようにコツが必要なものなどいろいろなので,いろいろな問題を解いて,媒介変数を消去するコツも身につけておきましょう。
それでは,これで回答を終わります。
これからも,『進研ゼミ高校講座』にしっかりと取り組んでいってくださいね。
















