4年生の難単元「２けたでわるわり算の筆算」のつまずき解消法とは？

4年生が２学期につまずきやすい「２けたでわるわり算の筆算」。
つまずきやすい４つのポイントとその解消法について詳しく解説していきます。

「２けたでわるわり算の筆算」でつまずくと、その先の算数でもつまずきやすい

４年生の２学期に学習することの多い「２けたでわるわり算の筆算」。「ニガテ」と感じるお子さまが多くいらっしゃるようです。
この「２けたでわるわり算の筆算」のニガテをそのままにしてしまうと、以降学習する単元「小数÷整数のわり算」でもニガテが生まれる原因に。５年生で学ぶ「小数のわり算」「割合」「速さ」「平均」「単位量あたりの大きさ」などの単元でもわり算を多用するので、ニガテの連鎖が続いてしまう前につまずきポイントを解消しましょう！

「２けたでわるわり算の筆算」のつまずきポイントとその解消法とは？

では具体的に、お子さまは「２けたでわるわり算の筆算」の学習のどこでつまずいてしまうのでしょうか。実は、「２けたでわるわり算の筆算」の計算を行うためにはたくさんの手順を踏まなければならず、お子さまが「難しい」と感じるポイントがそれぞれにあります。

＜つまずきポイントは以下の４つ！＞

① どこの数字を見比べて、どこに商をたてればよいのかわからない！

② 九九を唱えてたてる商を見つけることができない！

③ ２けた×１けたのかけ算を、正しく暗算できない！

④ 商が大きすぎたときに、どうしたらよいのかわからない！

まず１つ目のつまずきは「商をたてる位を判断する」ステップの際に発生しがちです。
「いったいどこの数字を見比べて、どこに商をたてればよいのかわからない」と感じてしまうのです。

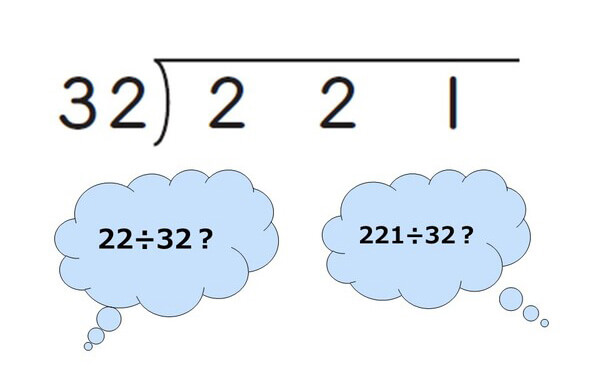
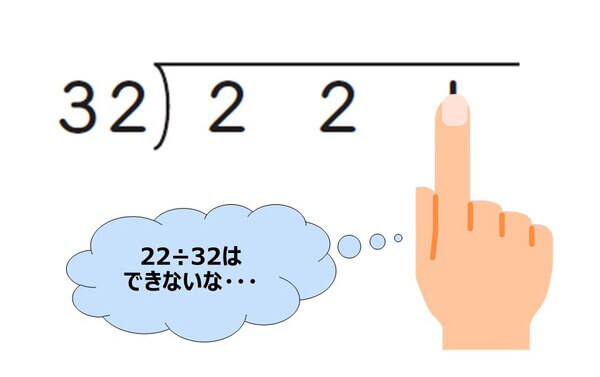
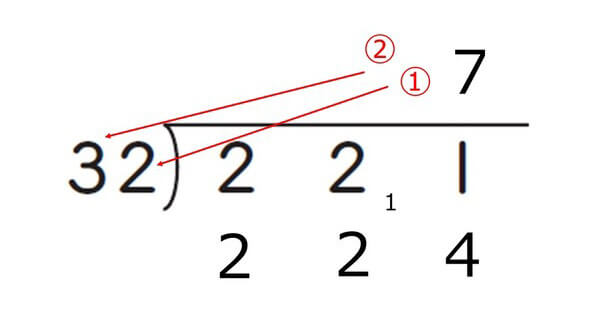
この場合のおすすめの解決方法は、「まず、見なくてもよい数字を一度指で隠してしまう」ことです。以下のように、一の位を指で隠して「22÷32」をしてみましょう。「それだとわれない」という場合には指を離し、今度は「221÷32」でわれるかどうか、再度確認しましょう。

次のステップでは「たてる商を考える」という作業をしますが、１けたでわる筆算の場合は、九九を唱えていけば商が見つかったのに対して、２けたでわる筆算の場合は、九九を唱えることができません。
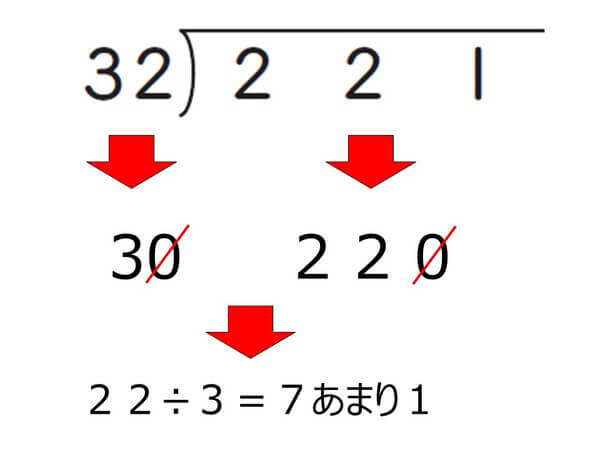
そのため２けたでわる場合は、「『わられる数』と『わる数』をそれぞれ概数でとらえ直してから、商を考える」必要があります。
今回の場合は、「221」と「32」をそれぞれ「220」と「30」ととらえ直したうえで「22÷３」の計算をする必要があります。

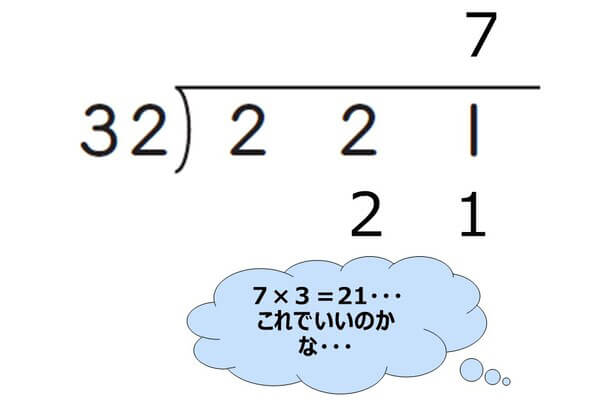
次のステップでは、「商にたてた数を、わる数にかける」という作業を行いますが、この際にも「２けた×１けたのかけ算が正しく暗算できない」というケースが発生しがちです。
今回の問題だと、まず「７×２」の計算をしたあとに「７×３」を計算するのが正しいのですが、その順番をまちがえてしまったり、かけ算の答えを書く位を誤ってしまったりするのです。

この場合の解決策としては、「手順に慣れるために、かけ算の筆算の反復演習をしっかりする」「くり上がりの数をメモする習慣をつける」といったことに取り組みましょう。

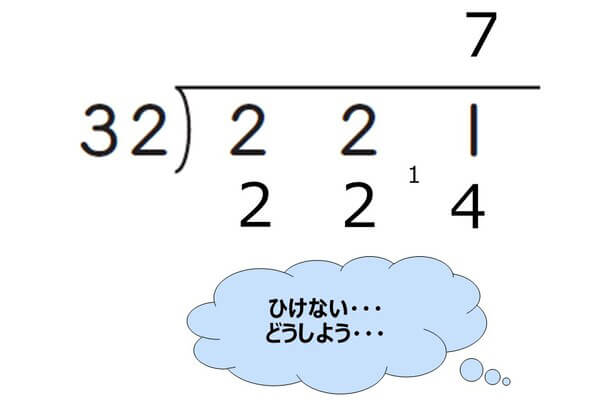
最後のステップとして、「たてた商が正しいかどうかひき算をして確かめて、適宜、商を直す」必要がありますが、「ひけないときに、どうしたらよいのかわからない」ために、とまどってしまうお子さまがいます。

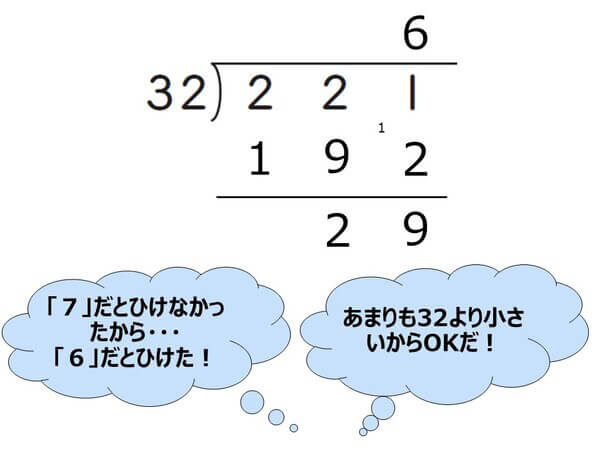
解決するためには、「商を修正する必要があるときの対応方法を知る」ことが重要です。「ひくことができない」ときには商を小さくする必要があり、逆に、「あまりが大きすぎる」ときには商を大きくする必要がある、ということをしっかりと覚えるようにしましょう。
また、あまりが大きすぎることに気がつかず、そのまま解答してしまうケースも少なくありません。「あまりが大きすぎないかどうか、最後にチェックする習慣」も身につけるようにしましょう。

「２けたでわるわり算の筆算」では、このようにたくさんの手順の中で、それぞれのつまずきポイントに注意しながら答えを求める必要があるため、ニガテに感じてしまうお子さまが多いのです。
ニガテをつくらないためには、前述の観点をしっかりおさえたうえで、くり返し問題に取り組む必要があります。

「進研ゼミ 小学講座」では、楽しみながら確実にわり算の力を伸ばしていける「わり算マスタープログラム」をご用意しています。「２けたでわるわり算の筆算」の学習は「わり算マスタープログラム」にお任せください！