主体的な学びを促す問いづくり②（高校数学編）

　第２回は、高校・数学の「背理法」「条件付き確率」を題材にした模擬授業が行われ、教科、学校段階を超えた問いづくりについて、高校の教員13名に、小・中学校の教員６名を加えた19名が集まり、議論した。

　※本勉強会は、2019年度に実施した「主体的な学び研究会」での成果を土台にスタート。第１回に続き、第２回もオンラインで実施。「ICEモデル」のフレームを活用した問いづくりの模擬授業を、参加した先生を生徒役として行い、その内容を基に議論していった。

　一つめの模擬授業を担当したのは、愛媛県・私立聖カタリナ学園高校の井上沙緒里先生。「背理法」を題材に取り上げ、生徒の主体的な学びを促す問いづくりを目標に掲げたオンライン模擬授業を行った。

　まず井上先生は、参加者に授業テーマを提示した。

　そして、井上先生は、映画『それでもボクはやってない』の紹介動画を見せ、問①として、「この映画を見たことがあるでしょうか。この映画の主人公のように、あなたがもし冤罪事件に巻き込まれてしまったら…どうやって自分の無実を証明しますか？」と参加者に問いかけ、30秒ほどで考えさせた。

　井上先生から指名された２名の参加者は、問①の答えを次のように発表した。

　参加者「真の犯人を捜します」
　参加者「優秀な弁護士を雇って、アリバイを全て出して証明したいと思います」

　次に、井上先生は、問②を投げかけた。

　少し考える時間を設けた後、井上先生は、「答えが出なくてもよいので、どのように考えたのか教えてください」と述べ、３名の参加者に答えを聞いた。

　参加者「一番信頼できる部下を信じます」
　参加者「どのように答えを出せばよいかわからず、混乱しています」
　参加者「部下ではなく、取引先相手に真実を聞いてもよいですか？」

　井上先生は、問①と問②の参加者の答えを受け、「問①では、真犯人を見つけたり、自分のアリバイを証明したりして無実を証明するという意見が挙がり、問②では、部下ではなく、取引先に話を聞くという意見が出ました。この二つの問いに共通する考え方は何だと思いますか？」と参加者に質問した。

　すると、参加者から「連れてきた証人や部下が嘘をつく可能性もあるということかと思いました」という声が挙がった。

　それを受けて、井上先生は「先ほど、問①の答えとして、自分の無実を証明するために、アリバイを全部出すと話してくれた方がいましたが、問①では、自分が有罪であると仮定し、それを否定するアリバイを出せばうまくいき、問②では、嘘をついている人を見破りたかったので、正直であることを否定すれば嘘を見抜くことができます。これが、今日の題材である『背理法』の考え方です」と話し、証明したいことの補集合を否定することが、背理法であると説明した。

　さらに、井上先生は、数学において背理法がどういう証明方法かを確認するため、教科書の例題を説明した。

　今回の参加者には、小・中学校の教員がいるため、高校数学の問題だけでは背理法を理解することが難しいと考え、さいころの例を挙げて，背理法で用いる補集合の考え方を説明した。

　井上先生は問①と問②、そして背理法の考えを土台として、問③について、参加者に考えてもらい、答えをチャット欄に記入してもらった。

　参加者からは、「決断する際の理屈づけ」「好きな子に告白する勇気」「たくさんある製品の中でどの製品を選ぶか」「旅行先でおみやげを買うとき、本当にこれでいいのかどうか」「仕事でうまくいかないときに、どうすれば乗り越えられるか」といった意見が挙がった。

　井上先生は、それらの回答を受け、次のように授業を締めくくった。
　「皆さん、すばらしい意見をありがとうございます。何らかの意思決定の際に、背理法が使えるのではないかと考えてくれたようです。数学を身近な場面で感じてもらえたらうれしいです」

　二つめの模擬授業を担当したのは、岡山県立岡山御津高校の笹埜圭亮先生だ。「条件付き確率」を題材にオンラインで模擬授業を行った。その内容は、「確率」の単元のまとめとして45分×２コマで実施予定の授業を、模擬授業用に20分間に短縮したものだ。

　まず笹埜先生は、「『条件付き確率』が日常生活でどのように活用できるのかを考えましょう」と授業のねらいを伝え、本時の学習事項に関する既習事項を確認した。

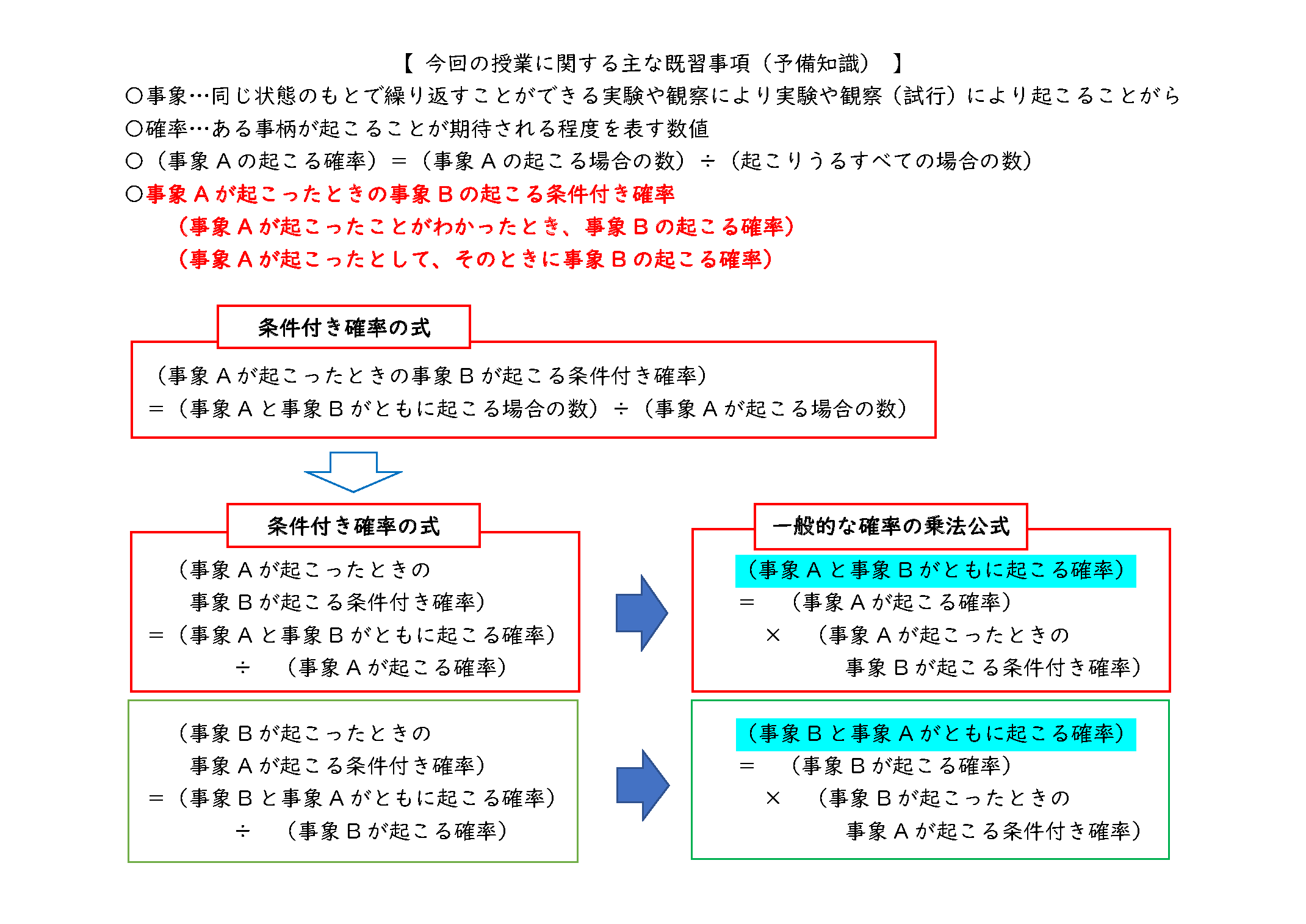
　次に、条件付き確率の応用である、「ベイズの定理」の公式を説明した。

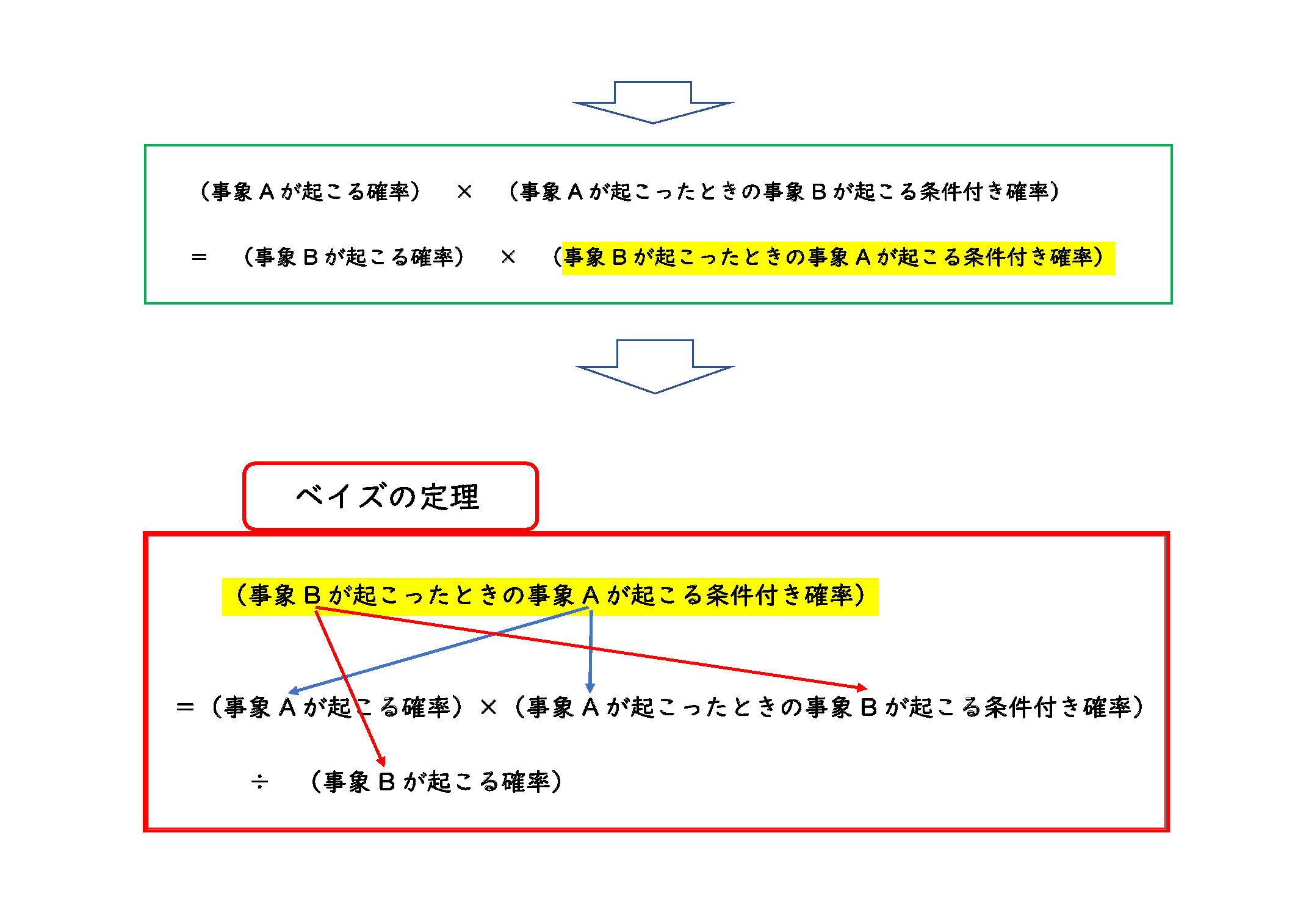
　そして、参加者が理解しやすいように、実際の確率と条件付き確率の求め方を、さいころやくじの例を挙げて説明した。

　笹埜先生は、「このように、確率の公式を用いて、確率の求め方を学習していきました。では、これからの社会でよりよく生きていくために、確率がどのように活用できるか、私たちの身近な場面から考えていきたいと思います」と述べ、場面設定を読み上げた。

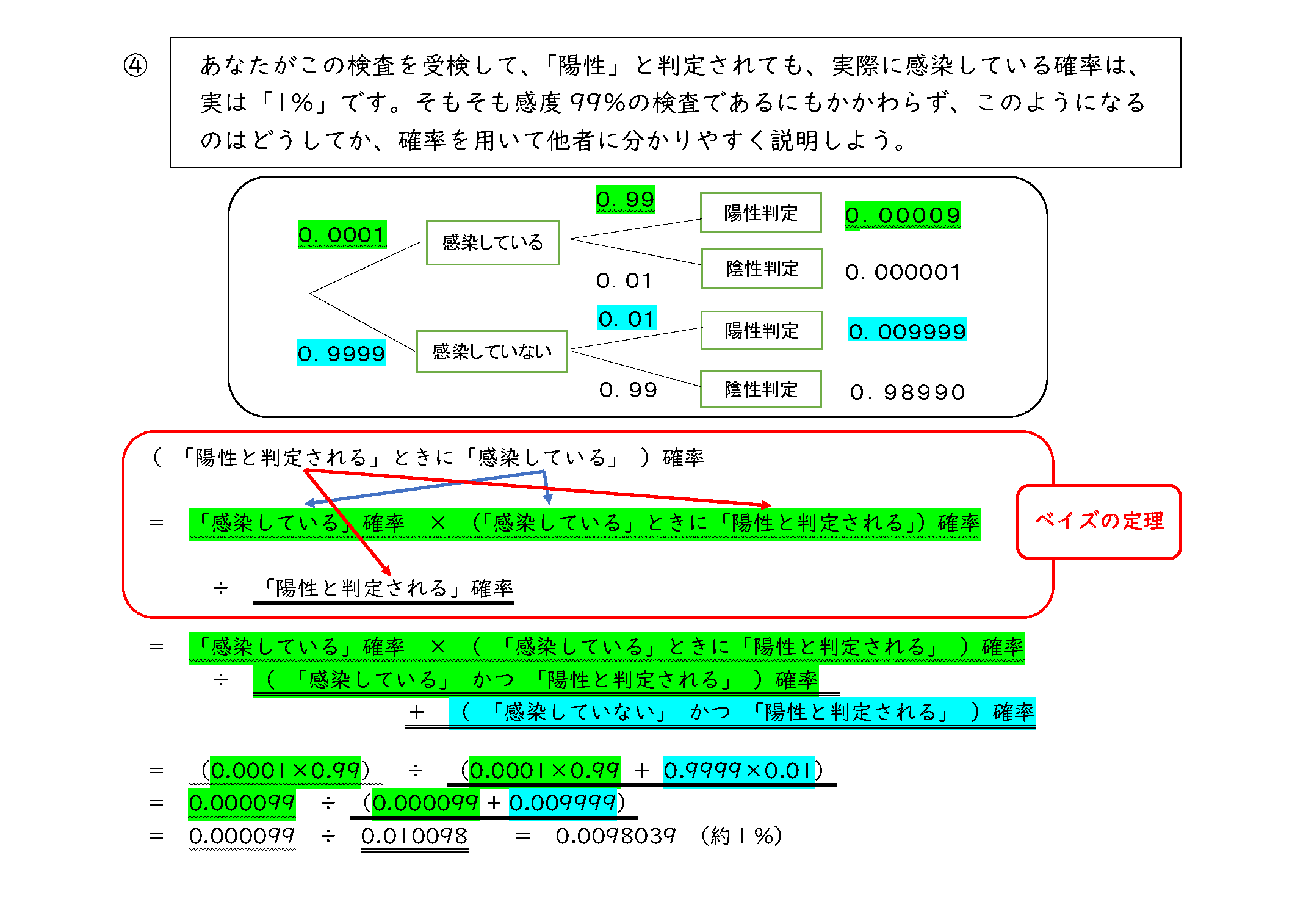
　笹埜先生は、新型のウイルスに関する感染について、確率を用いて解き明かすことを提案。参加者に問①を投げかけたが、すぐに答えられる参加者はいなかった。

　問①を解く前提として、条件付き確率を用いて考えられるようにするために、問②と問③を投げかけた。実際の授業では、生徒が考える時間を確保する予定だが、今回の模擬授業では、時間がないため、図解で求め方を説明した。

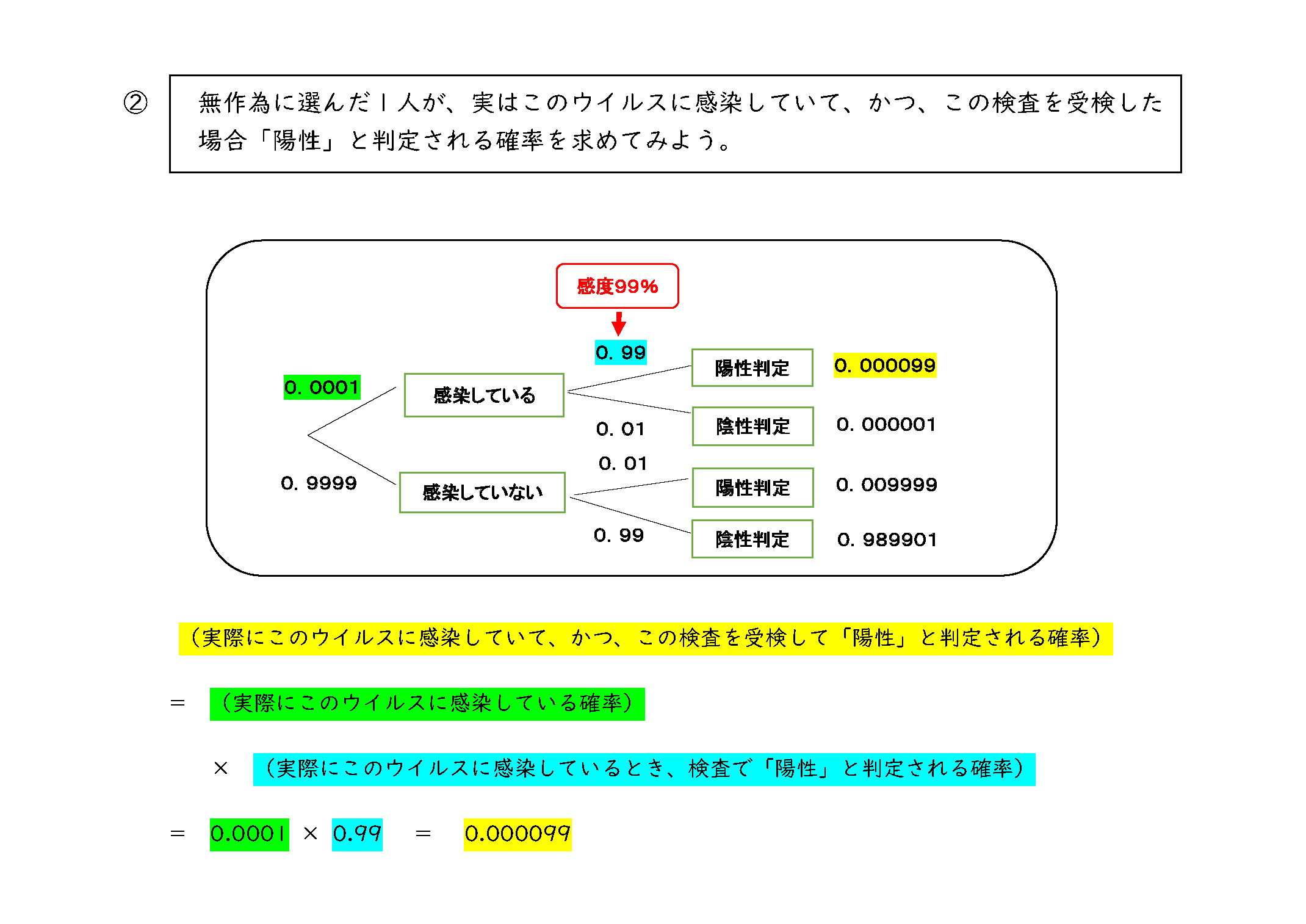
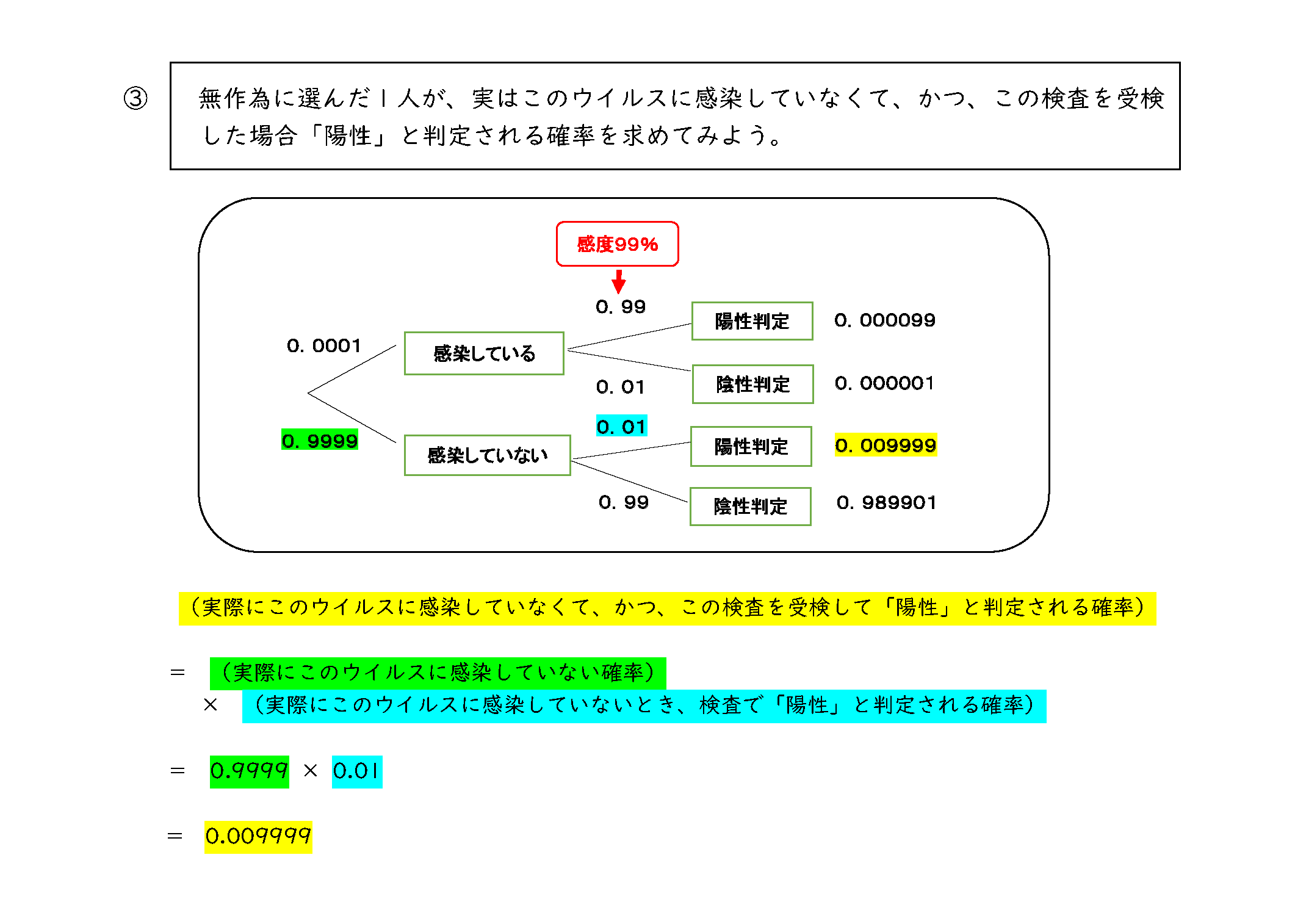
　その後、笹埜先生は「授業冒頭で投げかけた問①について考えたいと思います。この問題は、条件付き確率の応用であるベイズの定理を利用して計算すれば、正解は１％だと導くことができます」と話し、その求め方について解説した。

　笹埜先生は、これまで学んできた確率の知識をさらに応用できるようにするために、問⑤を投げかけ、チャット欄に考えを記入してもらった。

　すると、ある参加者から「検査の回数を増やして感度を高めればよいと思います」という声が挙がった。それに対して笹埜先生は、ほかにも「感染率を高めた状態で検査をする」「検査の特異度を高める」「検査の感度を高める」ことも可能だと述べた。

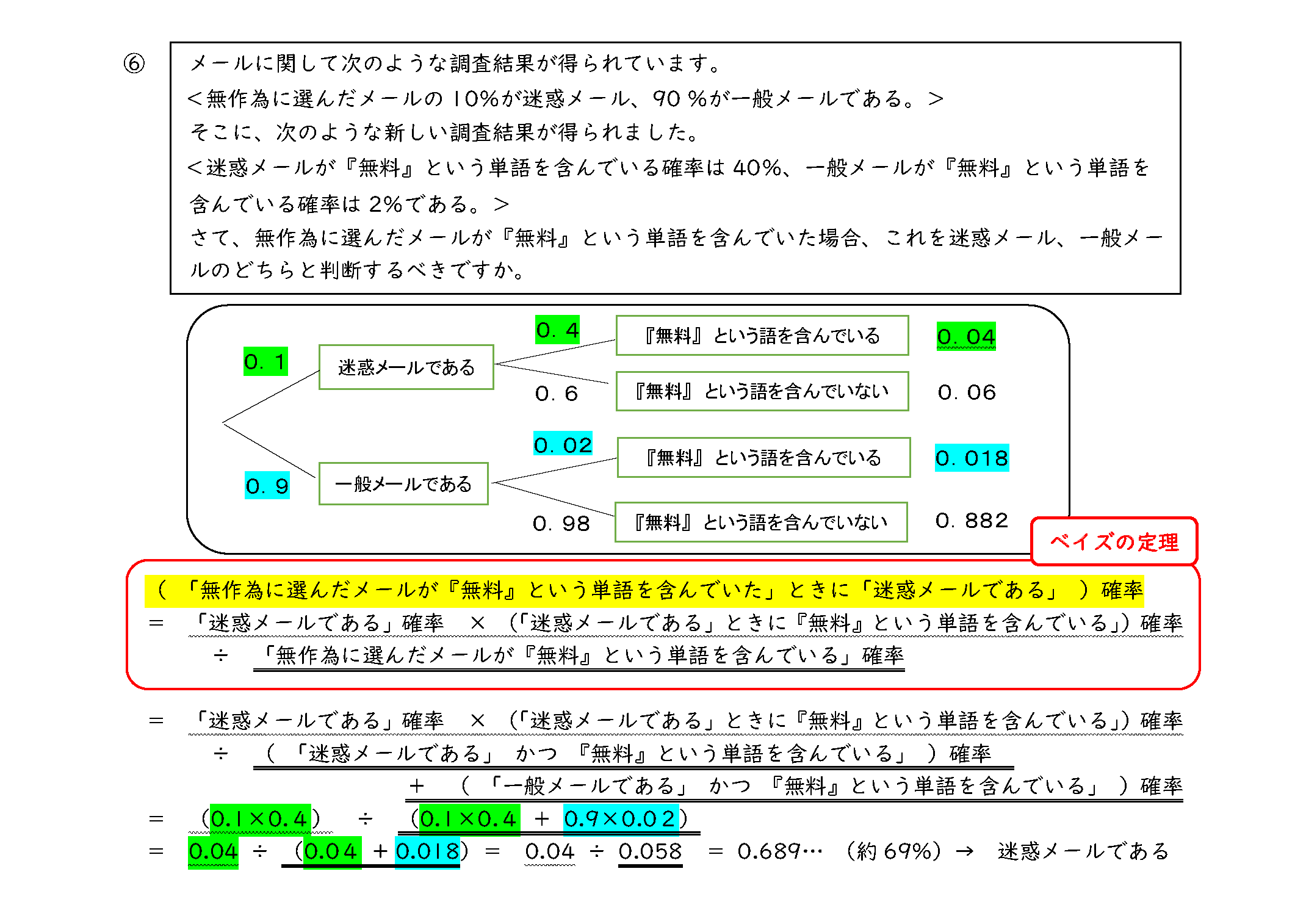
　ほかに、条件付き確率の活用例として迷惑メールに関する例を挙げ、ベイズの定理を用いて迷惑メールである確率を求めるにはどうするかを解説した。

　その後、笹埜先生は、確率を社会のどのような場面で生かせるのか、問⑦を出した。

　参加者からは、次のような意見が挙がった。

参加者「ドラフト会議で指名が重複した場合、意中の球団に入れる確率に役立つと考えました」
参加者「野球では、打率や出塁率を踏まえて打順を決める際に役立つと思います」
参加者「部活動で戦略を決める場面。例えば、サッカーでシュートの決定率などから、戦略を考えられるのではないかと思います」

　最後に笹埜先生は、条件付き確率の活用例を挙げ、何のために、どのように活用できるのかを説明し、「確率を活用して考えれば、状況を的確に解釈し、適切な判断をすることに役立ちます。過去の経験や情報、新たに得たデータを基に、そのときの最適解、納得できる解を導き出すことができるでしょう」と述べ、授業を締めくくった。

　模擬授業後には、元広島県立祇園北高校の柞磨昭孝先生のファシリテーションで、２名の授業者と参加者によるディスカッションが行われた。まず、模擬授業を担当した井上先生と笹埜先生が、今回の模擬授業の題材について述べた。

　井上先生は、「学習内容を生徒が自身の人生で生かせるようにするため、教科書の文脈を超えるような問いにするにはどうしたらよいのか悩みました。また、授業後に、背理法を活用し、生徒に何ができるようになってほしいのかが、私の中で明確になっていません」と、自身の課題について話した。

　笹埜先生は、生徒が探究したくなるような問いの設定や授業展開に課題を感じていると述べた。

　柞磨先生は、「今回の勉強会では、模擬授業で行った授業のフレームを他校種や他教科で活用する方法を探ることがねらいです。小学校や中学校の先生はいかがでしょうか」と、問いかけた。すると、次のような発言が挙がった。

　小学校教員「私は国語が専門で、数学が苦手です。数字から傾向をつかむことはできると思いますが、私自身は勘などから意思決定をすることが多いです。現在は、データ分析はAIに任せることもできます。自分のように算数や数学が苦手な子どもの主体性を、算数や数学で引き出すというのは難しいと感じました」

　それに対して笹埜先生は、「今回の授業の目標には、よりよく生きていくために、確率の考えのよさを生かしていくことを考えました。誰も正解が分からないこれからの社会において、納得解を得るためにデータの収集や分析の方法を学び、データから新しい価値を創造できるような人材を育成していきたいと考えています」と述べた。

　高校の数学教員からは、「例えば、プレゼンテーションをする際、数値で根拠を示すことは重要であり、多くの人に自分の考えを納得してもらうためには、数値は強力な武器になると思います」という声が挙がった。

　数学の重要性を多くの教員が感じていることから、それを児童・生徒にどう気づかせるかが議論の中心となった。ある参加者は次のように意見を述べた。

　参加者「『確率』とはどのようなものなのか、授業の中で生徒が実感できるかどうかがポイントだと思いました。その上で、生徒が『確率は日常生活でも使えるかも』と思えるようになることが重要ではないでしょうか」

　その意見を受け、柞磨先生は、「高校数学では学習事項が多く、教員は、限られた文脈の中で解き方を説明することで精いっぱいになりがちです。例えば、笹埜先生の授業では、確率の問題に、条件付き確率という異質なものが入ってきた際、生徒から問いが出てくるかどうかが重要だったのではないでしょうか」と述べた。

　生徒が主体的な問いを立てられるようになるためには、どうしたらよいのか、参加者はさらに議論を深めていった。参加者から、「どれほど数学が楽しいものなのか、教員が生徒に語ればよいのではないでしょうか」という提案があった。

　それについて、井上先生は、「私自身が数学を好きなことを語ったとしても、生徒は受け身でしかなく、やはり主体性を引き出すには、今日のように教員側から問いかける必要があると思います」と話し、問いの設定の難しさについて述べた。

　そうした意見を受け、ある参加者から、井上先生と笹埜先生に質問があった。
　「高校の数学において、公式や解法を生徒が使わざるを得ない場をつくるといった授業をデザインすることは難しいのでしょうか。授業にそうした場をつくることで、生徒から主体的な問いは出てくるのではないかと思いました」

　笹埜先生は、「公立の普通科高校では、そのようにじっくり問いをつくる時間を設けるのは、カリキュラム上、難しいかもしれません。一方、理数科などでは、数学の課題研究に取り組むことができると思います」と述べ、そうした取り組みを行うためには、教員のマインドセットも変える必要があると話した。

　参加者からは、「教員は、児童や生徒に知識を教え、それを生活でどう活用させるかという道筋で授業をデザインしています。しかし、それは教える側のねらいでしかありません。私たちが日常生活で何かを学びたいと思うのは、活用したいことを入り口としていることが多いはずです。教える側のねらいと学ぶ側とのベクトルが異なる点が課題ではないでしょうか」という指摘があった。

　柞磨先生は、その意見を受け、次のような問題点を示した。
「高校数学は、学びが体系化されており、指導が研究し尽くされ、解き方も洗練されています。そのため、数式を解くスキルを習得した方が大学入試には有利といえるため、教員が解法を説明しすぎているのではないでしょうか。算数や数学の授業で、『なぜこのようなことをやるのか』ということに児童や生徒が気づくよう、日常的に問いかけることが重要だと考えています」

　ある参加者は「総務省の統計局には、様々なデータが公開されています。生徒がそれらのデータを用いて問題をつくるという授業を行えば、より主体的な活動になるのではないでしょうか。また、先ほど確率の活用の場として『告白の成功率』を挙げた先生がいましたが、学校の体育館の裏と屋上ではどちらの方が成功率が高いかなどを調べたら面白いのではないでしょうか」と述べ、生徒が関心を持つデータを扱うことを提案した。

　別の参加者からは「高校時代の数学では、二次関数や三平方の定理などを分野ごとに学びましたが、それらを総合的に扱うような授業はありませんでした。今回の模擬授業のような授業を受けていたら、数学的な思考をもっと好きになっていたかもしれないと思いました」という声が挙がった。

　最後に、柞磨先生は次のように勉強会を締めくくった。
　「エドガー・ドガの『踊り子』という有名な絵では、主役の踊り子は右下に描かれ、その周囲にはたっぷりと余白が取られていて、彼女を値踏みする人などが描かれています。今回の授業では、『確率』が踊り子の部分だといえます。教員は『確率』そのものを教えることも大事ですが、工夫して余白のデザインを行い、生徒に確率の意義や価値を気づかせることが重要です。子どもが数学のスキルを使って合理的判断ができるようにしなければ、子どもが主体的に社会参画していく力は育ちません。各教科の授業において、リアリティーのある文脈をどのようにつくるかをさらに研究していく必要があるでしょう」

　【井上沙緒里先生】
　今回の勉強会から、リアリティーのある文脈と数学の本質をいかにつなぐかということが私にとっての明確な課題となりました。これまでの授業では、学んだ公式や定理をうまく活用させて複雑な問題を解くことに論点を置きがちであったように感じます。しかし、先生方との議論を通して、生徒の生きている現実社会とつながるようなリアリティーのある文脈から始まって、それを解決する場面で数学の本質に触れる、そして得たことから現実社会のものごとを生徒が自分なりに評価をするということが主体的な学びだと考えるようになりました。
　また、「Extensionsの問い」の先を考えたときに、生徒が社会参画し、よりよく生きていくには、どのような力を育てたいかという見通しを立てて授業の展開を考えるということも教えていただけました。さらに、小・中学校の先生との議論では、「主体的」や「問い」とは何なのかということも考えることができ、よい刺激になりました。

　【笹埜圭亮先生】
　今回の勉強会に参加させていただいて、高等学校の「数学科」で目指す「生徒自らが、問題の解決に向けて見通しをもち、粘り強く取り組み、問題解決の過程を振り返り、よりよく解決したり、新たな問いを見いだしたりするなど」の「主体的な学び」について考察を深めることができました。
　模擬授業では、本質目標を「確率の考え方のよさを生かして、確率を、よりよく生きるために自己の夢や目標を実現したり、最適解や納得解を導いたりするための意思決定に活用し、自立した社会の構成者となる」とし、「問いづくり」に挑戦しました。そして、教科や校種を超えた先生方とのやり取りをとおして、「社会参画を促す学びであったか」「フロー状態、夢中になる時間をどれくらいつくれたか」「そもそもなぜ条件付き確率を学ぶのか、生徒の中での納得感は得られたのか」「生徒自身が実感をもって『確率は使える』と思えたのか」などの課題を確認することができました。
　今後も引き続き、「主体的な学び」についての研究に精進したいと思います。