【評価・テスト】見えないものを測る Vol.5『テスト結果の見方とテストの妥当性』

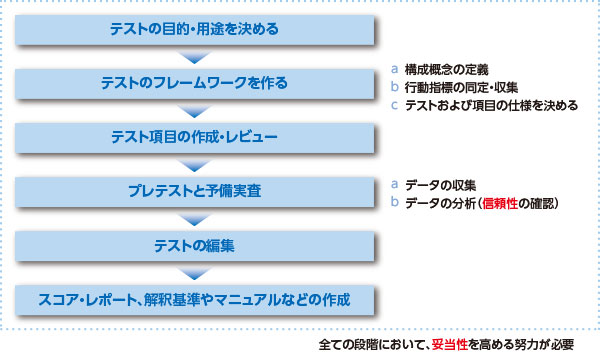
テスト作成のステップ
はい、ジュースで乾杯! 完成しましたよ!
乾杯からスタートですか! いただきます!
最初はテスト項目を30個準備しましたが、分析で不適切な項目を除いて、最終的には
20個でテストが完成しました
。信頼性も十分の、満足いくテストに仕上がったと思いますよ。今回のテスト作成では、この項目のセットを選ぶこと、順番を決めること、冊子に仕上げることが、テスト作成のステップの
「テストの編集」 に該当します。
そして、最後のステップの
「スコア・レポート、解釈基準やマニュアルなどの作成」 も、今回は、採点方法をまとめた簡単な説明書を作成し、これで完成しました。
今回のテストの採点方法は、各項目の選択肢に応じた0~4点を、20項目分、単純に合計するのでしたよね。
先生、早速自分でテストを受けて採点してみました。僕の得点は、80点満点中の40点でした。 僕もデータ分析をしたので、このテストの 「平均値」
は知っています。予備実査でこのテストを受けてもらった人たちのデータを最終版の20項目で採点し直したら、平均値は42.1点でしたよね。
平均が42.1点で、僕は40点。僕は平均以下、平均より劣っているという結果でした。地味にショックです…。
平均値、中央値、標準偏差
平均値と比べてショックを受けているのですね。
マナブさん、得点の低かった人から高かった人へと順番に並べたときに、ちょうど真ん中にくる人の得点を「中央値」といいますが、このテストの中央値は、38.0点でした。順番に並べた真ん中の38点より、マナブさんの40点は、高い得点ですよ。
え、そうなのですか!?
マナブさんが最初に比較した平均値は最も基本的な統計量で、確かに、あるテスト結果との比較の際によく使われます。しかし平均値はさまざまな得点結果を、半ば強引に1つにまとめ上げるための1つの方法に過ぎません。平均値と比較するだけでは、見えないこともたくさんあります。このことはぜひ、覚えておいてください。
具体例をあげて、平均値(mean)と中央値(median)の違いを見てみましょう。次の5つの点数があるとします。
1点、2点、2点、9点,10点
平均値は、各値の総和を値の個数で割ります。次の計算式のとおり、5つの値の平均値は4.8です。
(1+2+2+9+10)÷5 =4.8
中央値は、各値を小さい順に並べたときの真ん中の値です。値が全部で5個ある場合は、左から3番目の値です。上の例ではすでに小さい順に並んでいますので、左から3番目の2(点)が中央値です。
平均値だけでなく、中央値も見るほうがいいのですね。
できるだけ見るほうがいいですね。他にもいくつか大事な値はありますが、なかでも 「標準偏差」 はぜひ理解してください。大事なので説明しますね。ちなみに、このテストの標準偏差は14.6でした。
標準偏差ですか。前回出てきた「測定の標準誤差」と似た名前ですね。間違えそう…。
マナブさん、いいですね! そうです。
どちらも散らばり具合を表すもの です。似たものですよ。
測定の標準誤差は、真の値からの距離、標準偏差は、データの平均値からの距離 に基づいています。
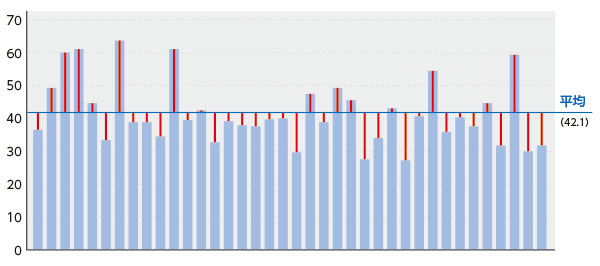
下の図を見てください。これはデータの一部ですが、一人ひとりの得点を棒グラフで示しています。図の中の青色の横線は、全体の平均値です。そして赤色の縦線が、平均値とデータ1つひとつとの距離を表しています。標準偏差とは、この赤線の距離それぞれの、いわば平均です。
もしデータの1つひとつが平均値と同じような値であれば、赤線が示す距離はみんな短くなり、そして標準偏差も低い値になります。
逆に、データの1つひとつが平均よりずっと大きかったりずっと小さかったりして平均から離れたものが多いと、赤線の距離が長いものが多いので、標準偏差は大きな値になります。つまり、
データの散らばり具合が大きいほど、標準偏差は大きくなる ということです。
標準偏差の図
もし分布が正規分布という標準的な形になっている場合、前回のコラム4で解説した測定の標準誤差と同じように、標準偏差も、平均値から標準偏差±1の範囲に約68%、±2の範囲に約95%の値が含まれると考えることができます。正規分布の場合は、分布の平均値と標準偏差が分かれば分布全体が分かり、ある得点が、分布全体の中でどの位置にいるかなどを把握することができます。
一方で、正規分布の形をしていない場合は上記の考えは当てはまりません。それでも、平均と標準偏差が分かれば、たとえば異なるテスト同士を比較し、それぞれの分布の違いを大まかに確認することができます。分布を要約する際の基本は、その中心(位置)と散らばり具合(散布度)を示すことですが、平均値と標準偏差はそれらを表す最も基本的な統計量です。
平均値、中央値、標準偏差…いくつかの基本情報は分かりました。でもそれらを値で聞いても、僕のレベルが全体のどのレベルなのか、まだピンと来ません…。
そうですね、平均値や標準偏差などの値は、分布のさまざまな情報のなかから1つの情報を取り出して表した値です。 「代表値」 と呼ばれていますね。複雑な情報を適切な代表値で要約することも重要なことですが、全体像を把握するには、 「度数分布」 を見ると分かりやすいと思いますよ。度数分布は、それぞれの得点区間に何人いるかを表したものです。それをグラフにしたものは、 度数分布図 とか、 ヒストグラム といいます。 では、このテストの度数分布図を見てみましょう。
度数分布図
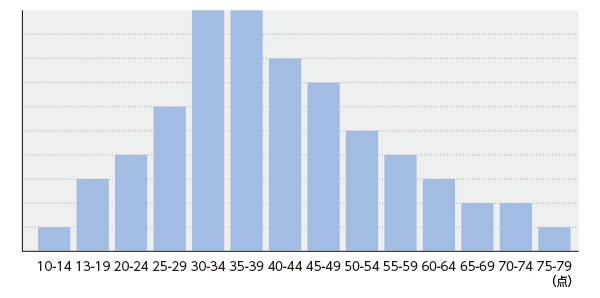
これは視覚的に分かりやすいですね。僕の40点を平均値42.1と比べると「平均以下」という印象が強かったのですが、この図で見ると、それほど劣った感じはしなくなりました。
でも、75点以上を取っている人もいるのですね! すごいなあ!
10点近い人から80点近い人まで、幅広くいましたね。そしてこの分布は山の形になっていますが、山の裾野は右のほうに広がっていますね。少数ながら、結構な高得点を取っている人が存在しているのが分かります。
世の中には、なかなかなツワモノがいるのですね…。そういえば先生、予備実査前に、この能力が高そうなグループを予想しましたよね。
ええ、今回のテストで測定するのは、社会に出たときに求められるコミュニケーション能力ですので、実際に社会に出たことがある、「インターンシップ経験者」が、高得点になるのではないかと予想しましたね。そして予備実査で、1週間以上のインターンシップ経験の有無についても尋ねました。
そうでしたよね。その結果って、どうでしたか?
えっとですね…・、はい! 1週間以上のインターンシップ経験の「ない」グループは、平均は41.0点、標準偏差は14.7で、経験の「ある」グループは、平均は52.5点、標準偏差は10.5でした。
うわ! やっぱりインターンシップ経験者の平均は高いのかっ!
構成概念どおりの能力が高そうな人が、実際にこのテストでも高い得点を取った のですね。これは、 このテストの妥当性を示すいい証拠 です。とても嬉しいことですよ。
テスト的にはよかったかもしれませんが…、僕としては、社会でそういう人たちと競わなければならないのかと思うと、憂鬱です。
ちなみに、高得点者がみんなインターンシップ経験者というわけでもなく、経験がなくても高得点の人もある程度いましたよ。
ですよね…。僕の得点レベルは全体での真ん中あたりではありますが、とにかく、僕よりもずっと高得点な人もそれなりにいるということで…。 先生、僕のこの結果を見たとき、僕のコミュニケーション能力は社会で通用するものになっているといえるんでしょうか? それとも…通用しないんでしょうか?
測りたかったものが測れたのか? ~テストの「妥当性」とは~
マナブさん、このテストでいえることは、他の 大学生と比べてマナブさんがどのレベルにいるか ということです。これは一種の相対評価ですね。一方で、 社会や組織が求めるレベルとの比較は絶対評価 となります。これは、私たちが現時点で持っている情報からは、残念ながらできません。
あ…。た、確かにそうでした…。最初に、もうすぐ社会に出る大学生の「言葉で、自分の考えを伝える力」の標準的なレベルと自分のレベルを比較して、自己理解につなげるためのテスト、と決めました。そしてそのとおりにできていますが、でも僕が本当に知りたかったのは、社会で通用するかどうかなのですが。う~ん…。
通用するかどうか、ですか。たとえば、大学生の中での上位○%の人を選抜するような使い方であれば、今のテストでもできるかもしれません。しかし、この得点から「○点を取れば○○ができる能力がある」という具体的な解釈をすることは、現状ではできません。そのような解釈基準は、また新たに計画を立てて、データを集めて、その結果から作っていくしかありませんね。
今までのテスト作成過程でも、構成概念を定義したり、妥当性を高めるための努力を続けてきました。それでもなお、このテストはマナブさんが
測りたかったものを本当に測れているのか、という反省点 が出てきましたね。これも 妥当性 の1つです。
妥当性の検証は開発段階で完結するものではなく、運用に入ってからも継続的に行っていく必要があります。テストの妥当性を高めるには、次のような努力が必要ということです。
テスト作成のすべてのステップにおいて、また、完成したテストの運用開始後も継続して、以下の観点を中心にエビデンスを収集・蓄積していく:
- テスト(項目)が、想定している構成概念を測定するものとして適切か(フレームワークと合致した内容・構造になっているか)
- 十分な精度の測定が実現できているか(信頼性)
- それらの結果として、テストが目的にかなう情報を提供できているか、あるいは期待された効果・影響を発揮しているか
テストを作るのって、大変…。
テストは目に見えない「構成概念」を測定する道具であるからこそ、妥当性の検証は、極めて重要なテーマです。
そしてテスト開発はまだまだ奥深く、楽しいですよ。
たとえば、今回のテストはごくシンプルにするために、 構成概念を絞りました 。理論も、 「古典的テスト理論」
という従来のものに基づきました。ですがテスト理論には、この他に、比較的新しい 「項目反応理論」 というものもあります。
従来のテスト理論である「古典的テスト理論」での限界に対応するために誕生したのが、「項目反応理論」(Item Response Theory: IRT)です。項目反応理論は、
- テスト項目の1つひとつから、「受検者の能力」と「項目の正答確率(期待値)」との関係性を推定し(見つけ出す)
- 関係性を推定した項目を大量に蓄えることで、その中から必要な項目を組み合わせて複数のテストを作ることができる
というものです。
これを実現するには相当数のデータが必要ですし、運用にも相当の覚悟が必要です。大変なものではありますが、もし実現できれば、たとえば次のようなテストの使い方が可能になります。
- 同質のテストを、項目を変えて何度も受検することができる
- 集団によってテストのレベルを調整でき(たとえばA校はやさしい項目を集め、B校は難しい項目を集めるなど)、そしてそれらの異なるテスト結果を相互に比較できる
- 受検者の回答パターンに応じて最適な項目を出題することで、少ない項目数、短時間で測定できる
そして、テストで測っておしまいではなく、その結果から何らかの評価につなげたいというマナブさんの考えは、大事なことだと思います。だから
次回はぜひ、このテストの解釈基準づくりも挑戦してみてください 。
テストの解釈基準を作るには、たとえばテストの高得点者は何ができているか、あるいは特定のスキルを持っていることが明らかな集団では何点ぐらい取れているか、といったデータを蓄積していきます。
次回、ですか…そうですね…微妙にモヤモヤが残るので、解釈基準づくりも挑戦したい気もします。
いいですね! 大学生のテスト結果での解釈基準を作るだけでなく、たとえば「企業が求めるレベル」を測るにはどうすればよいか、ということを考えるのも楽しいと思いますよ。
まだまだ、いろいろなテストの作り方や使い方があるのですね。先生、もしかしてこうなること、織り込み済みでした? 先生の策略どおり、この世界にはまり出したような気がします。
マナブさんの素質ですよ。実は初めてお見かけしたときから、マナブさんは将来、サイコメトリシャンになる道を目指す予感がしていましたよ!
さてこれからの就職活動ですが、私の研究所や、私が教えている大学院など、強くお勧めしますよ。
まさかこうなるとは…。でも、前向きに検討します! 研究所なら僕の「伝える力」でも通用しますか?
ですからそれは、実際に研究所に入って、ぜひ検証してみてください。
5回にわたりお届けしましたマナブコラム、いかがでしたか。ごく基本的で初歩的なテスト作りではありましたが、テスト作りの物語を通して、テストの信頼性や妥当性について、あるいはテスト結果の見方などに触れていただきました。最後に、読者の皆さんにけんたろう先生からメッセージがあります。
日常生活のなかで、人はさまざまなテストに出合います。自分がテストを受けなければいけないこともありますし、ニュースなどでテストの話題を目にすることも多いでしょう。一口にテストといってもさまざまですが、多くの大規模テストは、本コラムで紹介したような、非常に大変な手間をかけて作られています。大切なのは、目的に応じてきちんとテストが作られ、実施され、その結果が適切に利用されている(利用され得る)ということです。今後何かしらのテストに出合ったとき、このマナブコラムでお伝えした内容を踏まえて、クリティカルな視点でそのテストを眺められるようになっていただけたら幸いです。
- 分布の中心を表す統計として、平均値のほかに、中央値も見るほうがよい。
- 標準偏差は、データの散らばり具合を表す統計量である。
- テスト得点を目的に応じた形で解釈・利用できるかどうかは、それを裏付けるエビデンスがどれだけあるか(妥当性)によって決まる。
- テストの作成段階だけでなく、運用開始後も、妥当性を高める努力を継続的に行っていく必要がある。
プロフィール
加藤 健太郎
■専門領域
心理測定学および統計学
テスト理論に基づくテスト開発および関連する統計的手法の研究開発(サイコメトリシャン)
■やっていること
ベネッセ教育総合研究所におけるアセスメント研究開発
アセスメント事業の開発・運用サポート(ベネッセ、その他受託案件等)
最新の測定技術に関する情報収集・研究(学術論文・専門書の執筆、学会発表)
学術誌の論文査読委員
講演・研修会講師
大学非常勤講師
「テストについての正しい知識と、テストへのポジティブな興味関心をもっていただきたいと願っての連載です。テスト結果の数値の意味についても説明していこうと思います。次回以降もぜひ読んでみてください!」











