2019/04/24
事前・事後テストデザインにおける処遇効果の評価—事前テストの測定誤差の影響—
寄稿:宮﨑康夫(バージニア工科大学)
この度、アセスメント・教材研究開発室で心理測定の専門家による講演会
「事前・事後テストデザインにおける処遇効果の評価—事前テストの測定誤差の影響—」を開催しました。講演の詳細につきまして、講師の宮﨑康夫先生(バージニア工科大学准教授)から寄稿いただきましたので紹介いたします。
本稿では、事前テストにおける測定誤差が処遇効果の推定に与える影響について、事前・事後テストデザインを使ったプログラム評価研究の文脈において検討します。教育学・心理学研究においてはかなりの大きさの測定誤差がつきものであるのに、実務では、それを無視して、あるいはある程度の信頼性があるからそれでよしとして、簡便的な分析を行うことがよくあります。その頻用される簡便的な分析手続きが、プログラム評価などの処遇効果の推定等の研究に使われた場合に、どのような問題が起こるかを理解し、そのための何らかの措置を講じる必要性があることを喚起したいと思い、このテーマを選びました。
プログラム評価研究において、介入群と統制群との2群からなる事前・事後テストデザインは、処遇効果を評価するのに頻繁に利用される研究デザインの一つであり、そのような状況で多用される分析法として、事前テストを共変量として使う共分散分析(ANCOVA)があります。事前テストを共変量として使うことは、無作為割付(random assignment)が行われ、それが機能して処遇前のさまざまな特徴に群間差がない場合には、処遇効果の推定値の標準誤差を小さくし検定力を高めるのに役立ち、また、無作為割付が実施されなかったかあるいはされても何らかの理由で処遇前群間差が生じていた場合には、グループ間の処遇前の違いを調整し、統計的に等価な群の比較を可能とする目的で利用されます。
プログラム評価研究においては、時にその結果の社会的影響が強いことから、処遇効果の推定には正確を期すことが第一の用件となります。従って、プログラム評価研究では、その介入が原因で処遇効果が得られたとする因果推論を最終的にするため、研究デザインとして最も有効な無作為割付を用いることが大原則になります。
しかし、教育・心理学を含めた人間や人間を構成要素とする社会組織等を対象とする人間科学・社会科学分野における評価研究では、倫理的あるいは実施上の問題で現実には無作為割付が困難な場合も多くあります。あるいは、無作為割付を実施したにもかかわらずさまざまな理由で、分析の対象になっている特性を含めた諸特性の間に群間差が生じており、2群を平均的に統計的に等価にするという無作為割付の当初の目的が達成されていない場合もあります。そのような場合に、次善の策として講じられるのが共分散分析で、興味の中心である従属変数とて使われる事後テストと同じ特性を表す変数である事前テストを共変量として、介入前の群間差を統計的に制御するということがなされます。
1.重回帰分析における独立変数の測定誤差の取り扱いの現状
さて、2群からなる事前・事後テストデザインに適用される共分散分析は、事後テストを従属変数、そして被検者がどちらのグループに所属するかを示す0と1からなる質的変数であるダミー変数と、量的変数である事前テストとを2つの独立変数として行う重回帰分析の統計モデルです。重回帰分析モデルは、その中に分散分析や共分散分析をその特殊例として含む線型モデルであり、多くの分析法を包含する一般性があります。また、現象の予測や因子による説明、他の交烙因子(confounding factor)となる変数は、測定されていさえすれば、データ収集後でも共変量としてその影響を統計的に制御することができます。このように、重回帰分析モデルは現実の研究者の要請に応える柔軟性を持つモデルであるため、教育・心理・社会学研究を含めたすべての分野のデータ分析において、もっとも頻用される統計モデルであるといえます。
通常の重回帰分析モデルの結果が妥当なものとなるためには、いくつかの仮定が満たされている必要があります。その中で、重回帰分析を教育・心理・社会学等の人間や社会組織等を対象として扱う社会科学分野の研究に適用する際に特に重要と思われる仮定として、独立変数に測定誤差がない(Pedhazur, 1997; Lewis-Beck & Lewis-Beck, 2016; Fox, 2016; Cohen, J., Cohen, P., West, S. G., & Aiken, L. S., 2003 等参照) という仮定があります。しかしこの仮定は、現実的には、人間科学・社会科学分野ではまず完全に満たされていることはありません。なぜならば、知能や学力等の実際には観測できない構成概念を表す指標として、実際に観測できるテストの成績等をその代用として独立変数として使うので、偶然に伴う測定誤差が観測された変数には多かれ少なかれどうしても含まれてしまいます。そこで実際の実務では、信頼性係数が例えば0.8以上であれば、そのテストの成績は信頼できるとし、回帰モデルに持ち込み、そのあとはあたかもその変数に測定誤差がなかったかのように扱われることが通常よく行われています。
これを解決する一つの方法として、同一の因子の指標となっているとみなすことのできる複数の観測変数を使った因子モデルを持ち込んで、その因子間の回帰としてモデルを表現するJöreskogらによる構造方程式モデル(Structural Equation Modeling,SEM; SEMについては、例えば、Kline(2016)を参照)が開発された訳ですが、複数の指標を使っているため、どのようにして観測変数の測定誤差の悪影響が修正されるのかを単純明快に示すことは困難です。また、おもしろいことに、SEMは教育・心理・社会学では頻用されますが、計量経済学や一般統計学の分野で見ることは少なく、それよりも、測定誤差を含む一つの観測変数のみを使って、測定誤差の悪影響を取り除いて、処遇効果をバイアスなく推定する方法がErrors in Variable model (例えばWooldridge, 2016)としてより多く紹介されています。
2.重回帰分析における独立変数の測定誤差の影響
回帰分析において、従属変数にある測定誤差は、そのモデルにある残差項に含まれ、残差項は、他の測定されていないさまざまな要因からなる攪乱 (disturbance)項と従属変数の測定誤差との和となり、その二つに相関がない場合には、パラメータの推定値にバイアスを起こさないため、それほど深刻な問題を起きません。しかし一方で、独立変数に測定誤差があった場合には、パラメータの推定値にバイアスが起こり、このバイアスはサンプルサイズをどんなに大きくしても取り除けないものです(Greene, 2018)。測定誤差はどんな場合にも起こりますが、物を対象とする自然科学や工学、農学等の分野に比べて、人間や社会を研究の対象とする人間・社会科学では、能力、学習到達度、学業成績、性格傾向、価値観などの個人の属性、友人関係、夫婦関係、学級・学校風土、地域社会の連帯度、組織の結束力、さらにはより大きな組織の特性である社会の階層化度、国民性などの目に見えない、とらえどころのない構成概念が測定の対象であるため、それらの構成概念の測定には、身長や体重などの具体的な物理的な属性よりも、より大きな測定誤差が伴うことになります。そして、その測定誤差を多く含む構成概念を表す変数が回帰モデルの独立変数に使われれば、パラメータの推定値にバイアスがかかることになります。このことは、独立変数が一つの単回帰の場合にはよく知られており、その推定値の絶対値が母集団での真の値に比べて、0の方向に寄った値で推定されるので、希薄化と呼ばれています。教育・心理分野における古典的テスト理論では、このことを従属変数との相関係数でとらえて、相関係数の希薄化(attenuation)、そしてこれを信頼性係数で修正する手続きを希薄化の修正(correction for attenuation)と呼んでいます。これを、式で書いてみると以下のようになります。まず、正しいモデル、すなわちデータが発生したモデルは以下のようになります。
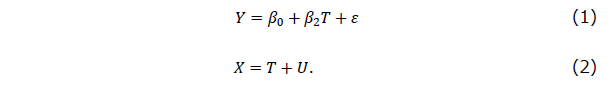
ここで、Yは観測された事後テストの点数、Xは観測された事前テストの点数で、その観測値には測定誤差が含まれており、したがって観測値Xは、その真の値Tとランダムな測定誤差Uからなっているとします。そして、式(1)は、事後テストが観測された事前テストの得点変数Xそのものでなく、測定誤差を含まない真の値Tに回帰され、その残差がεになります。ここで、式(1)の独立変数であるTと残差項εは独立、事前テストの真の値TとUは独立、Uとεも独立であると仮定します。さらには、残差項εは、平均は0、分散は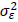 と仮定します。また、事前テストの測定誤差Uの平均は0、分散
と仮定します。また、事前テストの測定誤差Uの平均は0、分散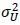 はであるとします。このように定義すると、事前テスト得点の信頼性係数λは、事前テストの観測値の分散を
はであるとします。このように定義すると、事前テスト得点の信頼性係数λは、事前テストの観測値の分散を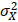 、事前テストの真値の分散を
、事前テストの真値の分散を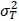 として、
として、
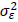 と仮定します。また、事前テストの測定誤差Uの平均は0、分散
と仮定します。また、事前テストの測定誤差Uの平均は0、分散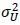 はであるとします。このように定義すると、事前テスト得点の信頼性係数λは、事前テストの観測値の分散を
はであるとします。このように定義すると、事前テスト得点の信頼性係数λは、事前テストの観測値の分散を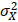 、事前テストの真値の分散を
、事前テストの真値の分散を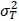 として、
として、
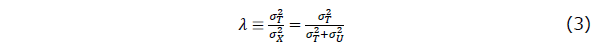
と表されることになります。信頼性係数 λ は、観測値の分散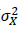 に対するその真の得点Tの分散
に対するその真の得点Tの分散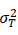 の割合なので、その範囲は、
の割合なので、その範囲は、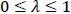 となります。つまり、テスト得点の変動が、すべて真値の変動によるもので、測定誤差の変動がないとき、完全に信頼できるテスト得点とみなせてλ=1となります。一方、テスト得点の変動が、すべて測定誤差の変動によるもので、真値の変動がないとき、λ=0となります。その範囲が0と1の間に収まるため、教育学・心理学では、λ≥0.8を大体の目安として良い信頼性を持つテスト得点などと呼んでいるわけです。
となります。つまり、テスト得点の変動が、すべて真値の変動によるもので、測定誤差の変動がないとき、完全に信頼できるテスト得点とみなせてλ=1となります。一方、テスト得点の変動が、すべて測定誤差の変動によるもので、真値の変動がないとき、λ=0となります。その範囲が0と1の間に収まるため、教育学・心理学では、λ≥0.8を大体の目安として良い信頼性を持つテスト得点などと呼んでいるわけです。
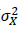 に対するその真の得点Tの分散
に対するその真の得点Tの分散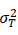 の割合なので、その範囲は、
の割合なので、その範囲は、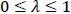 となります。つまり、テスト得点の変動が、すべて真値の変動によるもので、測定誤差の変動がないとき、完全に信頼できるテスト得点とみなせてλ=1となります。一方、テスト得点の変動が、すべて測定誤差の変動によるもので、真値の変動がないとき、λ=0となります。その範囲が0と1の間に収まるため、教育学・心理学では、λ≥0.8を大体の目安として良い信頼性を持つテスト得点などと呼んでいるわけです。
となります。つまり、テスト得点の変動が、すべて真値の変動によるもので、測定誤差の変動がないとき、完全に信頼できるテスト得点とみなせてλ=1となります。一方、テスト得点の変動が、すべて測定誤差の変動によるもので、真値の変動がないとき、λ=0となります。その範囲が0と1の間に収まるため、教育学・心理学では、λ≥0.8を大体の目安として良い信頼性を持つテスト得点などと呼んでいるわけです。
さて、事前テストに測定誤差があり、事前テストの観測値は式(2)で表されるように、その真の得点Tと測定誤差Uの和で発生しており、また式(1)で事後テストは、事前テストの真の値Tとの間の線型関係がある式(1)よりなる母集団からその観測値Yが発生しているとき、もしこれを誤って、事後テストの観測値Yを事前テストの観測値Xで回帰させ、それを通常の最小二乗法で推定したらどうなるでしょうか。これは、式でいうと、式(1)の回帰モデルでTを使う代わりに、Xを独立変数として使うということになるので、
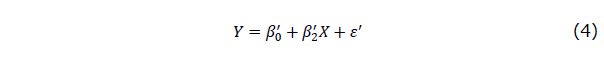
という単回帰分析を行うということになります。事前テストの回帰係数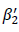 は、 期待値の代数的計算により、
は、 期待値の代数的計算により、
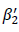 は、 期待値の代数的計算により、
は、 期待値の代数的計算により、
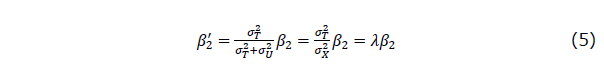
と表され、0≤λ≤1であることを考慮すると、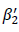 の(絶対値で表される) 大きさは、信頼度λに比例する分だけその真の値
の(絶対値で表される) 大きさは、信頼度λに比例する分だけその真の値 の大きさに比べて0に近い値になる、即ち希薄化が起こるということになるわけです。
の大きさに比べて0に近い値になる、即ち希薄化が起こるということになるわけです。
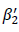 の(絶対値で表される) 大きさは、信頼度λに比例する分だけその真の値
の(絶対値で表される) 大きさは、信頼度λに比例する分だけその真の値 の大きさに比べて0に近い値になる、即ち希薄化が起こるということになるわけです。
の大きさに比べて0に近い値になる、即ち希薄化が起こるということになるわけです。
さて、上記で示したように、回帰分析で独立変数が一つの場合、独立変数に含まれる測定誤差がモデルのパラメータである回帰係数にもたらすバイアスは希薄化としてよく理解されてますが、独立変数が複数になった場合にはどうなるでしょうか。結論を先に述べると、いくつかの独立変数の中に、ただ一つでも測定誤差を持つ観測変数が含まれていると、その影響はその重回帰モデルにあるすべての回帰係数のパラメータに影響を及ぼし、バイアスがかかってしまうということになります。しかもどちらの方向にどの程度のバイアスがかかるのかは簡単には予測できないため(Greene, 2018, p.284)、これはかなりたちの悪い影響となります。このように重回帰分析は、さまざまな学問分野においておそらく最も有用な統計分析モデルでありますが、独立変数の一つにでも測定誤差があると、すべての回帰係数の推定にバイアスがかかってしまうという現実をDarlington (1990)は、重回帰モデルの最大の弱点と述べ(p.203)、この弱点克服のためのまだまだ多くの研究が必要だと指摘しています。
3.2群からなる事前・事後テストデザインの共分散分析のモデル
さて、この測定誤差の問題を、2群からなる事前・事後テストデザインに適用される共分散分析にあてはめるとどうなるでしょうか。共分散分析のモデルは、事後テストを従属変数、そして被検者のどちらのグループへの所属かを示す質的変数であるダミー変数(D)と、共変量として用いられる量的変数である事前テスト(X)とを二つの独立変数として行う重回帰分析の統計モデルです。それ以外の重回帰分析に必要な仮定、例えばモデルが正しく指定されているなどは満たされているとします。このモデルの正しい指定の仮定の一つとして共分散分析モデルの場合には、被検者のグループへの所属を表すダミー変数と事前テストの間には交互作用(interaction)はない、すなわち、二つの変数の積として表されるD × Xの項がモデルの中に入ってこないということがあります。いいかえれば、両グループとも事後テストの事前テストへの回帰係数が同じ、すなわち両群の回帰の傾きが同じであるということになります。現実のデータでは交互作用のある場合も多くみられるのですが、本稿では簡単のために、交互作用はないとします。これを、式で書いてみると以下のようになります。
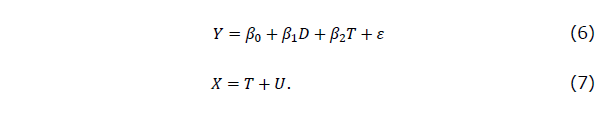
ここで、Yは観測された事後テストの点数、Dは介入群ではD = 1、統制群ではD = 0となるダミー変数、Xは観測された事前テストの得点で、その観測値には測定誤差が含まれており、したがって観測値Xは、その真の値Tとランダムな測定誤差Uからなっているとします。そして、式(6)は、事後テストが群を表すダミー変数Dと事前テストの測定誤差を含まない真の値Tに回帰され、その残差がεになります。ここで、式(6)の独立変数であるDやTと残差項εは独立、事前テストの真の値TとUは独立、Uとεも独立と仮定します。さらには、残差項εは、平均0、分散は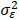 と仮定します。ダミー変数Dについては、サンプル数(N)の半分が介入群に、残りの半分が統制群に振り分けられたとすると、平均は、
と仮定します。ダミー変数Dについては、サンプル数(N)の半分が介入群に、残りの半分が統制群に振り分けられたとすると、平均は、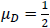 、分散は
、分散は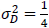 になります。また、事前テストの真の得点の平均は、介入群(グループ1)では
になります。また、事前テストの真の得点の平均は、介入群(グループ1)では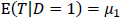 、統制群(グループ2)では
、統制群(グループ2)では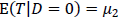 、そして、群内分散は同じで、
、そして、群内分散は同じで、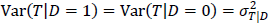 とします。また、事前テストの測定誤差の平均は0、分散は
とします。また、事前テストの測定誤差の平均は0、分散は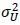 であるとします。
であるとします。
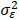 と仮定します。ダミー変数Dについては、サンプル数(N)の半分が介入群に、残りの半分が統制群に振り分けられたとすると、平均は、
と仮定します。ダミー変数Dについては、サンプル数(N)の半分が介入群に、残りの半分が統制群に振り分けられたとすると、平均は、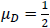 、分散は
、分散は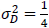 になります。また、事前テストの真の得点の平均は、介入群(グループ1)では
になります。また、事前テストの真の得点の平均は、介入群(グループ1)では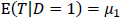 、統制群(グループ2)では
、統制群(グループ2)では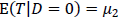 、そして、群内分散は同じで、
、そして、群内分散は同じで、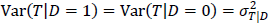 とします。また、事前テストの測定誤差の平均は0、分散は
とします。また、事前テストの測定誤差の平均は0、分散は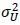 であるとします。
であるとします。
さて、この式(6)と(7)で表されたモデルを、2群からなる事前・事後テストデザインの観点から少し詳しく考えてみます。まず、測定誤差ですが、ダミー変数は、被検者がどちらのグループに入ったかを表す変数なので、これに関してはよほどのミスがない限り、測定誤差はないと考えられます。観測された事前テストの得点Xは、モデル式(7)で指定されたように、必ずある程度の誤差があると考えられます。
次に実験デザインについて考えてみます。本稿の最初に、得られた結果の影響力の大きいプログラム評価研究では、無作為割付を行うのが大原則であること、しかしまた、それが現実的には不可能な場合や無作為割付を行ってもそれがうまく機能していない場合も多いと述べました。その状況は、もし式(6)で考えていることが母集団で成り立っているような状況、即ち処遇前の群間差は事前テストのみで現れるという状況では、もし無作為割付が機能していれば、事前テストの真の得点の群間平均値差がない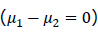 、あるいは群ダミー変数Dと事前テストの真の得点Tの間に相関がない
、あるいは群ダミー変数Dと事前テストの真の得点Tの間に相関がない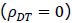 ということになります。一方、もし無作為割付が行われていないかそれがうまく機能していない場合は、事前テストの真の得点の群間平均値差がある
ということになります。一方、もし無作為割付が行われていないかそれがうまく機能していない場合は、事前テストの真の得点の群間平均値差がある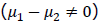 、あるいは群ダミー変数Dと事前テストの真の得点Tの間に相関が生じている
、あるいは群ダミー変数Dと事前テストの真の得点Tの間に相関が生じている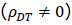 ということになります。
ということになります。
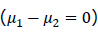 、あるいは群ダミー変数Dと事前テストの真の得点Tの間に相関がない
、あるいは群ダミー変数Dと事前テストの真の得点Tの間に相関がない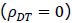 ということになります。一方、もし無作為割付が行われていないかそれがうまく機能していない場合は、事前テストの真の得点の群間平均値差がある
ということになります。一方、もし無作為割付が行われていないかそれがうまく機能していない場合は、事前テストの真の得点の群間平均値差がある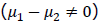 、あるいは群ダミー変数Dと事前テストの真の得点Tの間に相関が生じている
、あるいは群ダミー変数Dと事前テストの真の得点Tの間に相関が生じている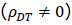 ということになります。
ということになります。
さて、式(6)は、Yの2つの独立変数DとTとによる重回帰モデルですが、共変量を事前テストの真の得点Tで調整して処置効果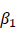 を推定するための共分散分析のモデルともみなすことができます。実際、このモデルが母集団で成り立っているとすると、
を推定するための共分散分析のモデルともみなすことができます。実際、このモデルが母集団で成り立っているとすると、
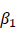 を推定するための共分散分析のモデルともみなすことができます。実際、このモデルが母集団で成り立っているとすると、
を推定するための共分散分析のモデルともみなすことができます。実際、このモデルが母集団で成り立っているとすると、
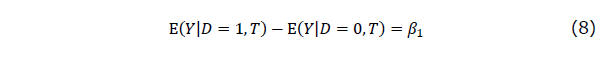
となり、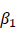 は事前テストの真値Tが同じだった場合の事後テストの平均群間差となるので、ダミー変数の回帰係数
は事前テストの真値Tが同じだった場合の事後テストの平均群間差となるので、ダミー変数の回帰係数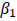 は確かに処遇効果を表していると解釈できます。
は確かに処遇効果を表していると解釈できます。
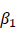 は事前テストの真値Tが同じだった場合の事後テストの平均群間差となるので、ダミー変数の回帰係数
は事前テストの真値Tが同じだった場合の事後テストの平均群間差となるので、ダミー変数の回帰係数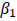 は確かに処遇効果を表していると解釈できます。
は確かに処遇効果を表していると解釈できます。
さてここで単回帰の場合にやったのと同じように、式(6)と(7)で表されたモデルが母集団でのデータ発生の真のモデルであった場合に、もし誤って観測された事前テストの点数Xには測定誤差はないとみなして、実際には測定誤差を含む事前テストの点数Xを使って、通常の共分散分析のモデルで分析を行ったら何が起こるかを考えて見ます。式でいうと、式(1)の回帰モデルでTを使う代わりに、Xを共変量として使うということになるので、
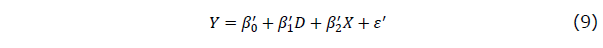
という重回帰分析を行うということになります。このときに、処遇効果を表すと考えられるダミー変数Dの回帰係数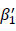 はどのように推定されるだろうか、その推定値にバイアス(偏り)はないのだろうかということを考えてみます。
はどのように推定されるだろうか、その推定値にバイアス(偏り)はないのだろうかということを考えてみます。
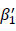 はどのように推定されるだろうか、その推定値にバイアス(偏り)はないのだろうかということを考えてみます。
はどのように推定されるだろうか、その推定値にバイアス(偏り)はないのだろうかということを考えてみます。
4.シミュレーションによるデモンストレーション
回帰係数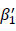 の推定値に起こるバイアスについて、実は、1変数の場合と同様に期待値を考える代数的な方法で、解析的に導くことができます。しかし、本稿では、実際にデータを発生させ、それを式(9)のモデルに適用した最小2乗法による回帰分析を数多く行い、その結果をまとめるというシミュレーションを行いました。回帰係数の推定値のバイアスの方向や大きさ等について、同じデータを構造方程式モデルで分析した結果と比較して示したいと思います。
の推定値に起こるバイアスについて、実は、1変数の場合と同様に期待値を考える代数的な方法で、解析的に導くことができます。しかし、本稿では、実際にデータを発生させ、それを式(9)のモデルに適用した最小2乗法による回帰分析を数多く行い、その結果をまとめるというシミュレーションを行いました。回帰係数の推定値のバイアスの方向や大きさ等について、同じデータを構造方程式モデルで分析した結果と比較して示したいと思います。
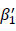 の推定値に起こるバイアスについて、実は、1変数の場合と同様に期待値を考える代数的な方法で、解析的に導くことができます。しかし、本稿では、実際にデータを発生させ、それを式(9)のモデルに適用した最小2乗法による回帰分析を数多く行い、その結果をまとめるというシミュレーションを行いました。回帰係数の推定値のバイアスの方向や大きさ等について、同じデータを構造方程式モデルで分析した結果と比較して示したいと思います。
の推定値に起こるバイアスについて、実は、1変数の場合と同様に期待値を考える代数的な方法で、解析的に導くことができます。しかし、本稿では、実際にデータを発生させ、それを式(9)のモデルに適用した最小2乗法による回帰分析を数多く行い、その結果をまとめるというシミュレーションを行いました。回帰係数の推定値のバイアスの方向や大きさ等について、同じデータを構造方程式モデルで分析した結果と比較して示したいと思います。
モデルのパス図
母集団から式(6)と(7)で表されるモデルによりデータが発生したとします。パス図で表すと図1のようになります。
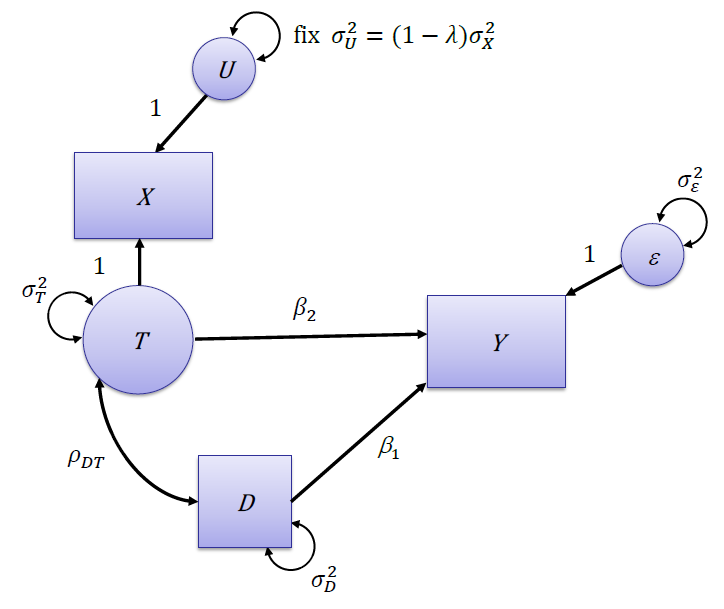
図1.Xに測定誤差を含む構造方程式モデルのパス図
このパス図は、構造方程式モデリングの表記方法に従い、四角(または長方形)は観測されている変数を表し、丸(または楕円)は観測されていない潜在変数を表します。観測された事前テストX、事後テストY、そして群ダミー変数Dは観測されているので四角で、事前テストの真の得点T、その測定誤差U、そして事後テストに付随している残差εは、観測されていない潜在変数なので丸で表現されています。ここで仮定として、この事前テストの信頼性係数λの真の値は、他の研究より知られているとします。また、片方向の矢印はその影響の及ぼす方向性を表し、そのそばに式(6)と式(7)中に現れている回帰係数が記されています。また2つの変数をつなぐ両方向の矢印はその2変数間の相関を、1変数につながっている両方向の矢印は、その変数分散を表し、それぞれ横にその大きさを記号で表示してあります。
最後に、図中に事前テストの誤差Uの所には、Fixとあります。これは、この図で構造方程式モデルを最尤法で推定する場合には、このモデルには一つの潜在変数Tに対してその指標となる変数(indicator variables)が一つしかなく、このままではモデルが同定(identify)されないので、それを解消するために、この研究の外部で得られている情報であるこの事前テストの信頼性係数λを使って、事前テストの誤差分散パラメータ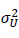 を、
を、
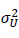 を、
を、
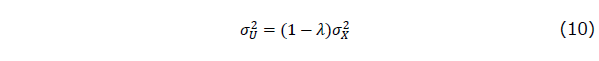
で求めて、固定(fix)してしまうことを表しています。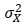 は観測された事前テストXの母分散なので、データが得られた状況ではその推定値である標本分散
は観測された事前テストXの母分散なので、データが得られた状況ではその推定値である標本分散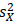 で置き換えて使うことになります。
で置き換えて使うことになります。
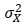 は観測された事前テストXの母分散なので、データが得られた状況ではその推定値である標本分散
は観測された事前テストXの母分散なので、データが得られた状況ではその推定値である標本分散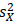 で置き換えて使うことになります。
で置き換えて使うことになります。
シミュレーションデザイン
上で述べたように、2つの要因、すなわち(a).信頼性係数λで記述される事前テストの測定誤差の程度と、(b).事前テストの真の得点の群間平均値差(ダミー変数Dと事前テストの真の得点Tの間の相関係数の大きさ)で表される無作為割付の成功度の程度について、もし誤って事前テストの観測変数を共変量として共分散分析で処遇効果を推定してしまった場合にどのような影響が現れるかを見るために、シミュレーション条件を次のように設定しました(表1)。


まず、事前テストの信頼性係数(λ)については、一般に最低限信頼性があると認めれる(λ=0.7)、よい信頼性(λ=0.8)、非常に良い信頼性(λ=0.9)、測定誤差なし(λ=1)の4つのケースを考えます。次に、事前テストの真の得点の標準化された群間差(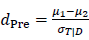 、ここで
、ここで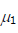 は介入群(群1)の事前テストの真の得点の平均、
は介入群(群1)の事前テストの真の得点の平均、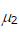 は統制群(群2)の事前テストの真の得点の平均を表す)をコーエンの効果量dの解釈に従って、小(0.2)、中(0.5)、大(0.8)を考え、どちらが大きいのかによって結果が変わる可能性を考慮し、そのマイナス符号のケースも考慮しました。それに加えて、無作為割付が成功し処遇前の事前テストの真の得点の群間差の平均がない場合
は統制群(群2)の事前テストの真の得点の平均を表す)をコーエンの効果量dの解釈に従って、小(0.2)、中(0.5)、大(0.8)を考え、どちらが大きいのかによって結果が変わる可能性を考慮し、そのマイナス符号のケースも考慮しました。それに加えて、無作為割付が成功し処遇前の事前テストの真の得点の群間差の平均がない場合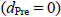 を考えます。以上の2つの要因がこのシミュレーションでの主要な独立変数ですが、構造方程式モデリングは比較的大きなサンプルサイズのデータの分析にうまく機能するということも知られておりますので、サンプルサイズも変化させました。一群あたり(N/2),35,70, 150 (2群合算で N= 70, 140, 300)と3つの異なるサンプルサイズの場合を用意し、小、中、大のサンプルサイズのケースと名づけます。残りの要因として、事前テストの真の得点と事後テストの観測値との相関
を考えます。以上の2つの要因がこのシミュレーションでの主要な独立変数ですが、構造方程式モデリングは比較的大きなサンプルサイズのデータの分析にうまく機能するということも知られておりますので、サンプルサイズも変化させました。一群あたり(N/2),35,70, 150 (2群合算で N= 70, 140, 300)と3つの異なるサンプルサイズの場合を用意し、小、中、大のサンプルサイズのケースと名づけます。残りの要因として、事前テストの真の得点と事後テストの観測値との相関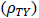 の大きさが考えられますが、ここでは
の大きさが考えられますが、ここでは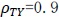 と比較的高い値に固定したケースを報告します(本稿では学力テストを考えているので、相関はある程度の高い正の値を考えてよいかと思います)。最後に、各グループの事前・事後に測定される同じテストの真の得点は、統制群(群2)で変化なし、介入群(群1)で事後テストが5点(各郡における真の得点平均の標準化された変化量を d とすると、d = 0.5)上がったとしてデータを発生させています。
と比較的高い値に固定したケースを報告します(本稿では学力テストを考えているので、相関はある程度の高い正の値を考えてよいかと思います)。最後に、各グループの事前・事後に測定される同じテストの真の得点は、統制群(群2)で変化なし、介入群(群1)で事後テストが5点(各郡における真の得点平均の標準化された変化量を d とすると、d = 0.5)上がったとしてデータを発生させています。
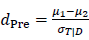 、ここで
、ここで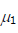 は介入群(群1)の事前テストの真の得点の平均、
は介入群(群1)の事前テストの真の得点の平均、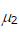 は統制群(群2)の事前テストの真の得点の平均を表す)をコーエンの効果量dの解釈に従って、小(0.2)、中(0.5)、大(0.8)を考え、どちらが大きいのかによって結果が変わる可能性を考慮し、そのマイナス符号のケースも考慮しました。それに加えて、無作為割付が成功し処遇前の事前テストの真の得点の群間差の平均がない場合
は統制群(群2)の事前テストの真の得点の平均を表す)をコーエンの効果量dの解釈に従って、小(0.2)、中(0.5)、大(0.8)を考え、どちらが大きいのかによって結果が変わる可能性を考慮し、そのマイナス符号のケースも考慮しました。それに加えて、無作為割付が成功し処遇前の事前テストの真の得点の群間差の平均がない場合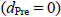 を考えます。以上の2つの要因がこのシミュレーションでの主要な独立変数ですが、構造方程式モデリングは比較的大きなサンプルサイズのデータの分析にうまく機能するということも知られておりますので、サンプルサイズも変化させました。一群あたり(N/2),35,70, 150 (2群合算で N= 70, 140, 300)と3つの異なるサンプルサイズの場合を用意し、小、中、大のサンプルサイズのケースと名づけます。残りの要因として、事前テストの真の得点と事後テストの観測値との相関
を考えます。以上の2つの要因がこのシミュレーションでの主要な独立変数ですが、構造方程式モデリングは比較的大きなサンプルサイズのデータの分析にうまく機能するということも知られておりますので、サンプルサイズも変化させました。一群あたり(N/2),35,70, 150 (2群合算で N= 70, 140, 300)と3つの異なるサンプルサイズの場合を用意し、小、中、大のサンプルサイズのケースと名づけます。残りの要因として、事前テストの真の得点と事後テストの観測値との相関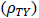 の大きさが考えられますが、ここでは
の大きさが考えられますが、ここでは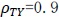 と比較的高い値に固定したケースを報告します(本稿では学力テストを考えているので、相関はある程度の高い正の値を考えてよいかと思います)。最後に、各グループの事前・事後に測定される同じテストの真の得点は、統制群(群2)で変化なし、介入群(群1)で事後テストが5点(各郡における真の得点平均の標準化された変化量を d とすると、d = 0.5)上がったとしてデータを発生させています。
と比較的高い値に固定したケースを報告します(本稿では学力テストを考えているので、相関はある程度の高い正の値を考えてよいかと思います)。最後に、各グループの事前・事後に測定される同じテストの真の得点は、統制群(群2)で変化なし、介入群(群1)で事後テストが5点(各郡における真の得点平均の標準化された変化量を d とすると、d = 0.5)上がったとしてデータを発生させています。
5.結果
シミュレーションの介入効果として解釈されるパラメータであるモデル中の群ダミー変数Dの回帰係数のバイアスに関する 結果を図2-aにまとめました。パネル上側にあるModel.Regと名付けられたものが、共分散分析(即ち回帰)モデルでの、下側のModel.SEMと名づけられたものが、構造方程式モデル(SEM)で分析された場合の回帰係数のバイアスを表しています。また縦3列に入っている35, 70, 150という数字は一群あたりのサンプルサイズを表しています。さらには、6個の各グラフの縦軸はパラメータ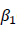 の推定値のバイアス(Bias)を、横軸は事前テストの真の得点の標準化された群間差
の推定値のバイアス(Bias)を、横軸は事前テストの真の得点の標準化された群間差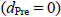 を表しています。そして、それぞれのグラフには、4つの信頼性係数(λ = 0.7, 0.8, 0.9, 1.0) ごとの関係が表示されています。
を表しています。そして、それぞれのグラフには、4つの信頼性係数(λ = 0.7, 0.8, 0.9, 1.0) ごとの関係が表示されています。
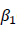 の推定値のバイアス(Bias)を、横軸は事前テストの真の得点の標準化された群間差
の推定値のバイアス(Bias)を、横軸は事前テストの真の得点の標準化された群間差 を表しています。そして、それぞれのグラフには、4つの信頼性係数(λ = 0.7, 0.8, 0.9, 1.0) ごとの関係が表示されています。
を表しています。そして、それぞれのグラフには、4つの信頼性係数(λ = 0.7, 0.8, 0.9, 1.0) ごとの関係が表示されています。
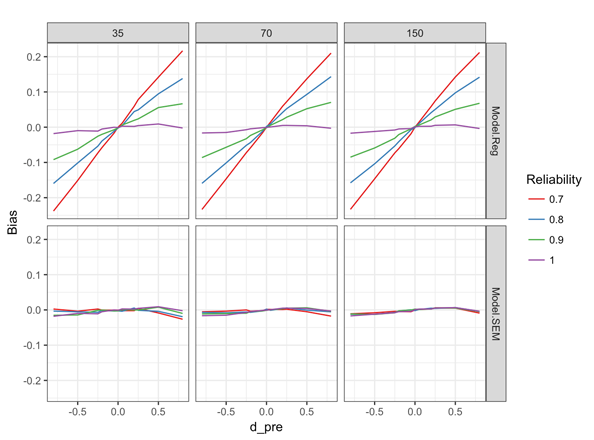
この図より以下のことがわかります。
(1) 構造方程式モデルで推定した場合は、信頼性係数の値、事前テストの真の得点の値、そしてサンプルサイズにかかわらず、バイアスは出ない (図2-aの下のパネルの3つの図で、どれも線がほぼBias=0の傾きのない直線となっていることより)。
(2) 事前テストの信頼性係数が1の時、つまり共変量が誤差なく測定されていれば、共分散分析モデルでも処遇効果をバイアスなく推定することができる (図2-aの上のパネルの3つの図で、それぞれの中心あたりにあるReliability = 1 の時のほぼ水平な直線を参照)。
(3) また一方今度は、事前テストの真の得点の平均に群間差がない場合 は、どの線も原点を通っていることより、処遇前に、事前テストの平均に差がない場合には、事前テストの測定誤差は、処遇効果の推定値にバイアスを引き起こさない。
は、どの線も原点を通っていることより、処遇前に、事前テストの平均に差がない場合には、事前テストの測定誤差は、処遇効果の推定値にバイアスを引き起こさない。
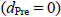 は、どの線も原点を通っていることより、処遇前に、事前テストの平均に差がない場合には、事前テストの測定誤差は、処遇効果の推定値にバイアスを引き起こさない。
は、どの線も原点を通っていることより、処遇前に、事前テストの平均に差がない場合には、事前テストの測定誤差は、処遇効果の推定値にバイアスを引き起こさない。
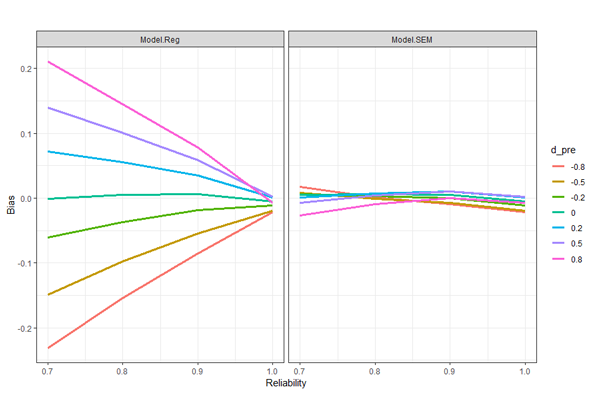
さて(3)の結論については、上記のグラフでは、事前テストの信頼性係数λの影響の詳しい様子がややわかりにくいので、各群のサンプルサイズが35人(両群合計で70人)の場合のみ、今度は横軸を信頼性係数(Reliability)として、プロットしたのが図2-bです。この図で、左側にある通常の回帰分析(Model.Reg)での分析結果で、ちょうど真ん中あたりにある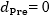 の線を見ると、これがReliability が0.7から1.0の間を変化するときにほぼBias = 0 の水平な直線となっています。このことより、もし事前テストの真の得点に群間差がなければ
の線を見ると、これがReliability が0.7から1.0の間を変化するときにほぼBias = 0 の水平な直線となっています。このことより、もし事前テストの真の得点に群間差がなければ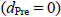 、即ち無作為割付がうまくいっていれば、誤差を含む観測された事前テストを共変量として使っても、処遇効果の推定値にバイアスが出ないこと、しかも、それは事前テストの信頼度がいくらであっても出ないことを示しています。
、即ち無作為割付がうまくいっていれば、誤差を含む観測された事前テストを共変量として使っても、処遇効果の推定値にバイアスが出ないこと、しかも、それは事前テストの信頼度がいくらであっても出ないことを示しています。
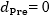 の線を見ると、これがReliability が0.7から1.0の間を変化するときにほぼBias = 0 の水平な直線となっています。このことより、もし事前テストの真の得点に群間差がなければ
の線を見ると、これがReliability が0.7から1.0の間を変化するときにほぼBias = 0 の水平な直線となっています。このことより、もし事前テストの真の得点に群間差がなければ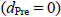 、即ち無作為割付がうまくいっていれば、誤差を含む観測された事前テストを共変量として使っても、処遇効果の推定値にバイアスが出ないこと、しかも、それは事前テストの信頼度がいくらであっても出ないことを示しています。
、即ち無作為割付がうまくいっていれば、誤差を含む観測された事前テストを共変量として使っても、処遇効果の推定値にバイアスが出ないこと、しかも、それは事前テストの信頼度がいくらであっても出ないことを示しています。

再び図2-aに注意をもどします。
(4) 最後に、図2-aの上側、Model.Regのパネル図から見て取れることは、ANCOVAの回帰分析では、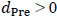 の時は、プラスの方向にバイアスが生じ、逆に、
の時は、プラスの方向にバイアスが生じ、逆に、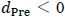 の時は、マイナスの方向にバイアスが生じていることです。そして、そのバイアスの大きさは、
の時は、マイナスの方向にバイアスが生じていることです。そして、そのバイアスの大きさは、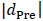 が大きければ大きいほど、
が大きければ大きいほど、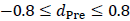 の範囲ではほぼ直線的な関係で、大きくなっていきます。これが実質的にどの程度の大きさのバイアスであるのかを評価するために、
の範囲ではほぼ直線的な関係で、大きくなっていきます。これが実質的にどの程度の大きさのバイアスであるのかを評価するために、 を
を の推定値とし、その真の値に対する相対バイアスを
の推定値とし、その真の値に対する相対バイアスを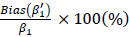 で定義すると、プラス方向のバイアスの最大値 0.211 (図2-bの左上) の相対バイアスは36.1%、また絶対値が最大となるマイナス方向のバイアス-0.232 (図2-bの左下) の相対バイアスは-39.8%となり、実質的にもかなりの大きさのバイアスであることがわかります。なお
で定義すると、プラス方向のバイアスの最大値 0.211 (図2-bの左上) の相対バイアスは36.1%、また絶対値が最大となるマイナス方向のバイアス-0.232 (図2-bの左下) の相対バイアスは-39.8%となり、実質的にもかなりの大きさのバイアスであることがわかります。なお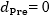 の時は、(3)で述べたように、Reliability が0.7から1.0の範囲では、その値がどの値であろうともバイアスに関しては0になっています。
の時は、(3)で述べたように、Reliability が0.7から1.0の範囲では、その値がどの値であろうともバイアスに関しては0になっています。
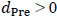 の時は、プラスの方向にバイアスが生じ、逆に、
の時は、プラスの方向にバイアスが生じ、逆に、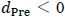 の時は、マイナスの方向にバイアスが生じていることです。そして、そのバイアスの大きさは、
の時は、マイナスの方向にバイアスが生じていることです。そして、そのバイアスの大きさは、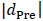 が大きければ大きいほど、
が大きければ大きいほど、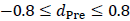 の範囲ではほぼ直線的な関係で、大きくなっていきます。これが実質的にどの程度の大きさのバイアスであるのかを評価するために、
の範囲ではほぼ直線的な関係で、大きくなっていきます。これが実質的にどの程度の大きさのバイアスであるのかを評価するために、 を
を の推定値とし、その真の値に対する相対バイアスを
の推定値とし、その真の値に対する相対バイアスを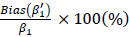 で定義すると、プラス方向のバイアスの最大値 0.211 (図2-bの左上) の相対バイアスは36.1%、また絶対値が最大となるマイナス方向のバイアス-0.232 (図2-bの左下) の相対バイアスは-39.8%となり、実質的にもかなりの大きさのバイアスであることがわかります。なお
で定義すると、プラス方向のバイアスの最大値 0.211 (図2-bの左上) の相対バイアスは36.1%、また絶対値が最大となるマイナス方向のバイアス-0.232 (図2-bの左下) の相対バイアスは-39.8%となり、実質的にもかなりの大きさのバイアスであることがわかります。なお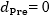 の時は、(3)で述べたように、Reliability が0.7から1.0の範囲では、その値がどの値であろうともバイアスに関しては0になっています。
の時は、(3)で述べたように、Reliability が0.7から1.0の範囲では、その値がどの値であろうともバイアスに関しては0になっています。
ところで、ここで示した図は従属変数とY (事後テスト得点)と独立変数T (事前テスト得点の真の値)が0.9の場合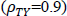 だけを示しましたが、他の場合でも似たような傾向を示しました。
だけを示しましたが、他の場合でも似たような傾向を示しました。
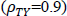 だけを示しましたが、他の場合でも似たような傾向を示しました。
だけを示しましたが、他の場合でも似たような傾向を示しました。
6.考察
結果(1)は、「測定誤差のある独立変数で回帰分析を行うと回帰係数の推定値にバイアスが生じることを防ぐ」ことが、構造方程式モデル(SEM)がJöreskogらによって開発された一つの動機であったことを考えると、なるほど確かにSEMは、独立変数に測定誤差のある場合に、処遇効果の不偏推定値を得るのに大変有効であるということがわかります。
結果(2)は、事前テストに測定誤差がないということは、すべての独立変数に測定誤差がないとする重回帰モデルの仮定が成立していることになるので、これは当然の結果です。
結果(3)は、事前テストの真の値に群間差がないことは、無作為割付が成功していることを意味しているので、無作為割付によって処遇前の両群の特性が同等になっていることを意味しています。無作為割付によって処遇前の両群の特性が同等になっていれば、事前テストの測定誤差は処遇効果の推定値のバイアスに全く影響を及ぼさなくなる、という結果は、だからこそ無作為割付が、処遇効果の評価研究においては、大いに推奨される大原則になっているといえます。
結果(4)は、処遇前に介入群の方が統制群よりも事前テストの真の平均点が高かった場合には、処遇効果を過大評価してしまう、一方逆に、処遇前に介入群の方が統制群よりも事前テストの真の平均点が低かった場合には、真の処遇効果を過少評価してしまうということを意味しています。さて、この後者のケースに関しては現実の例として、Campbell & Erlebacher (1970)やCampbell & Boruch (1976)らの報告を紹介します。彼らは、低所得者層の3歳から4歳の就学前幼児を対象にアメリカ合衆国連邦政府が1960年代の半ばから行って現在も続けられている、集団生活への適応力の養成を含めた学校教育へのレディネスを高め後の正規学校教育での成功の可能性を高めるための無料就学前援助補償教育プログラムであるヘッドスタート(Head Start)に対して行われたそのプログラムの効果の評価研究の結論が、効果がないかあるいは害でもありうるということであったのに対して、それが誤りである可能性があることを指摘しています。その理由として、ヘッドスタートへの参加は無作為割付ではなく、介入群に入る子供は統制群の子供に対して、介入前よりもともと学力が低く、その処遇前の両群の違いを制御する目的で、学力と比較的強い正の相関のある親の社会経済的地位でマッチングや共分散分析が施されたのだが、その制御に使われた共変量である社会経済的地位には測定誤差がかなりの割合で含まれているので、本稿で説明した処遇前に群間差が存在し、しかも共変量に測定誤差があるケースに生じるバイアスを挙げています。そしてヘッドスタートのケースでは、介入群の方が統制群に比べて共変量として使われた社会経済的地位の平均が低いので、そのバイアスはマイナスの方向に起こっており、それがヘッドスタートプログラムに実際はプラスの効果があっても、統計分析の結果は、誤って効果がないと出たり、極端な場合には負の効果があるとの結果が出る原因になっている可能性があると述べています。この推論は、ちょうど本稿の結果(4)で、処遇前に介入群の方が統制群よりも事前テストの真の平均点が低かった場合には、真の処遇効果を過少評価してしまうということに対応しています。ヘッドスタートのように国レベルで巨額の国家予算を使って行われる教育・社会政策プログラムは、その評価の結果により予算がカットされたり、あるいはプログラム自体を終了するということの起こる多くの人たちに影響力の高いハイステークスなものであるので、誤った処遇効果の推定値から、誤った政策決定を行ってしまうことの影響力は甚大です。多少の過少効果や過大評価であれば、政策決定には大きな影響はないが、共変量の測定誤差には、プラスの効果のあるプログラムが効果なし、あるいはマイナスの効果があると判断される可能性を引き起こすことがあるので、特に注意が必要であるといえます。
7.結論・まとめ
本稿では、無作為割付の成功の度合いと共変量に含まれる測定誤差の2つの要因が、処遇効果の推定にどういう影響を及ぼすかについて検討しました。新しい知見として、介入群の事前テストの平均値が統制群のそれより大きい場合には、効果が過大評価される、逆に介入群の事前テストの平均値が統制群のそれより小さい場合には、効果が過小評価される、極端な場合には、プラスの効果のある処遇がマイナスであるとの結果が出ることもあり得る、そしてそのバイアスの度合いは、事前テストの平均の群間差で表される無作為割付の不成功の度合いが大きければ大きいほど、そして事前テストに含まれる測定誤差が大きければ多いほど、大きくなることがわかりました。さらに、そのバイアスの度合いは、現実的にもかなり大きくものであること、例えば、通常はその得点は最低限信頼できるものであるとされる信頼性係数の値が0.7であっても、処遇前に得られる事前テストの平均値の群間差が大きいとき (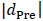 = 0.8) には、35%-40%のかなりの大きさのバイアスが生じることがわかりました。このことから、実際のプログラム評価研究の場面では、事前テストの平均の群間差の方向と大きさ、そして事前テストの信頼性の両方に注意を払い、どちらかの条件の完全性が崩れている場合には、通常の共分散分析では処遇効果の推定値にある程度のバイアスが生じてしまうことを念頭に置き、それに対して構造方程式モデルを使う等の何らかの適切な対処を講じることが必要と思われます。
= 0.8) には、35%-40%のかなりの大きさのバイアスが生じることがわかりました。このことから、実際のプログラム評価研究の場面では、事前テストの平均の群間差の方向と大きさ、そして事前テストの信頼性の両方に注意を払い、どちらかの条件の完全性が崩れている場合には、通常の共分散分析では処遇効果の推定値にある程度のバイアスが生じてしまうことを念頭に置き、それに対して構造方程式モデルを使う等の何らかの適切な対処を講じることが必要と思われます。
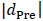 = 0.8) には、35%-40%のかなりの大きさのバイアスが生じることがわかりました。このことから、実際のプログラム評価研究の場面では、事前テストの平均の群間差の方向と大きさ、そして事前テストの信頼性の両方に注意を払い、どちらかの条件の完全性が崩れている場合には、通常の共分散分析では処遇効果の推定値にある程度のバイアスが生じてしまうことを念頭に置き、それに対して構造方程式モデルを使う等の何らかの適切な対処を講じることが必要と思われます。
= 0.8) には、35%-40%のかなりの大きさのバイアスが生じることがわかりました。このことから、実際のプログラム評価研究の場面では、事前テストの平均の群間差の方向と大きさ、そして事前テストの信頼性の両方に注意を払い、どちらかの条件の完全性が崩れている場合には、通常の共分散分析では処遇効果の推定値にある程度のバイアスが生じてしまうことを念頭に置き、それに対して構造方程式モデルを使う等の何らかの適切な対処を講じることが必要と思われます。
参考文献










