【調査研究】 「使える数学力」は身についているか —大学生調査から見える課題— （後編）

　本稿では、「使える数学力」について、当研究所で開発しているアセスメントとこれを用いた調査の結果について報告している。後編の今回は、「大学生の力の実態」について報告する。
※本稿の内容は、日本数学教育学会の論文誌『数学教育学論究』に掲載された「大学生の数理活用力を測るアセスメントに関する研究」から抜粋したものである。詳しくはそちらを参照いただければ幸いである。

　前編において、当研究所で開発している「数理活用力のアセスメント問題」の概要を示した。2012年には、この問題を大学生に実際に解いてもらう調査を行った。調査の参加者は123の大学に通う大学1～4年生666人であり、その内訳は、おおむね首都圏の大学生の属性を代表したものとなっていた。
　調査結果は項目反応理論を用いて分析し、受検者それぞれが数理活用力をどの程度持っているのかを示す得点（能力値）を算出した。この得点を6つのレベル（レベル1未満～レベル5）に区切り、受検者の大学生がどのレベルにあるのかを、主な学部系統ごとにまとめたものが図2である。また、図2の各レベルの受検者が「どのようなことができるのか」を記述したものを表2に示した。表2は、各問題の解答結果の分析を通して数理活用力の構成要素を抽出しレベルに基づき構造化したものである。

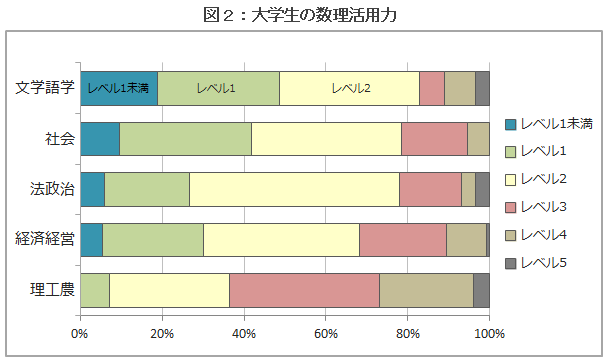
　図2を見ると、文系の学部では、ほとんどの学生がレベル3にたどり着いていないことがわかる。表2にある通り、レベル3は「平均や変化率などを用いた事象の比較ができること」という程度であり、必ずしも難しい数学が必要になっているわけではない。大学生であることを考えると、多くの人がこのレベルに到達していないということはやや不安が残る結果ではないだろうか。また、図2からは理系の学生でも多くがレベル４に届いていないことがわかる。レベル４も「単位当たり量や三角比を使いこなしたり、多様なグラフを利用したりできる」という程度であり、高度であるとは言い難いだろう。

　この結果は、社会の中で「使える数学力」の育成における課題を提示していると考えられる。表2において各レベルを特徴づけている知識や概念は、必ずしも高度ではないものの大学生の数理活用力を決定づける鍵となっている。これは、こうした知識や概念を、数学内の問題だけでなく幅広い状況の中で活用していくことの難しさを改めて示しているといえるだろう。カリキュラムの設計においては「新たな知識や概念の習得」が重視されることが多いが、それだけでなく数理活用力の評価軸を設け、その伸長を目標とした学習の機会を設けていくことが求められるのではないだろうか。社会の中で真に「使える数学力」の育成を、初等・中等教育ならびに大学教育の段階において考えていくべきときにきているのではないだろうか。