【場合の数と確率】条件つき確率の解き方について
確率の乗法定理についてですが,全体的に意味がよくわからないんです・・・
なぜn(A∩B)が4なのかとか,その他諸々理解ができません。改めて解説してください。
また,条件つき確率において,計算式の導き方も教えていただけると嬉しいです。
よろしくお願いします。
進研ゼミからの回答
こんにちは。
いただいた質問について, 早速, 回答いたします。
【質問内容】
【問題】
1から9までの数字が1つずつ書かれた9枚のカードから, 同時に2枚を引く。引いたカードの数字がどちら
も奇数であるとき, そのうちの1枚が5のカードである確率を求めよ。
【解答解説】から抜粋部分

確立の乗法定理について, 意味がよくわからない。

というご質問ですね。
【質問への回答】
2つの事象をA, Bとおくと, 求める確率は次の通りです。
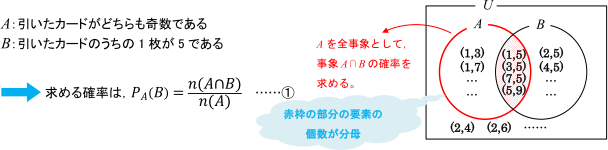
つまり,
「引いた2枚のカードがどちらも奇数」という条件がついた中での「1枚が5である」確率を求める
のが今回の問いです。
だから, 2枚のカードのすべての取り出し方に対する確率ではなく, すべての取り出し方のうちの「2枚がとも
に奇数である場合」に限定し, その中での確率を求めています。
すべての取り出し方に対する確率を求めることを単に「確率」と言うのに対し, 今回のように, すべての取り出
し方の中でも「2枚がともに奇数である場合」に限るという条件をつけ, その中での確率を求めることを「条件
つき確率」と言います。
そして, これらを理解したうえで, ①の分母・分子にあたる「場合の数」をそれぞれ求めてみましょう!
≪分母→引いたカードがどちらも奇数になるのは…≫
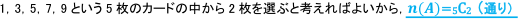
≪分子→引いたカードが5と奇数になるのは…≫
2枚のカードは同時に引くから, 2枚がともに5になることはなく,
2枚のカードは, (5と5以外の奇数)という組み合わせになります。
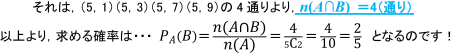
【学習アドバイス】
以上で説明を終わりますが, どうでしょう…わかりましたか?

これからも『進研ゼミ高校講座』を大いに活用し, あなたの学習に役立ててくださいね。













