【場合の数と確率】順列と組合せの見分け方
順列と組合せが問題を読んで、どちらを利用すれば良いのかわからない。
進研ゼミからの回答
こんにちは。
質問をいただいていましたので、お答えします。
【質問の確認】
問題を読んでも、順列と組合せのどちらの式を利用すればいいかわからない。ということですね。
【解説】
まず、順列と組合せについて正しく理解しましょう。
《順列》
一般に、いくつかのものを、順序をつけて1列にならべた配列を順列と
いうのでしたね。異なるn個のものから、異なるr個とった順列といい
その総数をnPrで表します。なお、
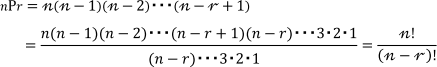
《組合せ》
一般に、異なるn個のものから、順序を問題にしないで異なるr個をとって
1組としたものを、n個のものからr個とった組合せといい、その総数は
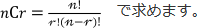
つまり、順列では、並べる順序を問題にして考えますが、組合せでは順序を
問題にしないで取り出し方だけを問題にして考えます。
したがって、順序が問題になる取り出し方の場合は順列で、順序が問題に
ならない取り出し方の場合は組合せで考えればいいわけです。
では、問題を考えてみましょう。
1(1)は「第1走者から第4走者までの4人を選ぶ・・・」
つまり、順序が問題になるので、『順列』の考えで。
4は「男子6人、女子10人の中から男子3人、女子4人を選ぶ・・・」
で、順序は問題にしていないので、『組合せ』の考えということになります。参考にしてください。
【アドバイス】
順列と組合せの定義を正しく理解して、教材も参考にしながらもう一度、問題を考えてみましょう。
これからも「進研ゼミ 高校講座」でがんばりましょう。













