【微分法(III)】複雑な関数のグラフのかき方
最大値や最小値を求める問題でグラフを考えたのですが,ちゃんと微分をして増減表をかいてグラフを考えても,答えのグラフと違ってしまいます。どうやったら正しいグラフがかけるのですか?
進研ゼミからの回答
こんにちは。
いただいた質問について,さっそく回答いたします。
【質問の確認】
最大値や最小値を求める問題で,微分をして増減表をかいてグラフを考えても,答えのグラフと違ってしまいます。どうやったら正しいグラフがかけるのですか?
というご質問ですね。
【解説】
2次関数や3次関数のグラフはだいたいの形が決まっていますが, 複雑な関数のグラフは, 増減だけでは正確な形がわかりません。それでは, 増減のほかに何を調べたらよいか, 具体的な例を見てみましょう。
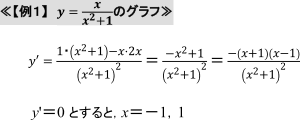
これより, yの増減表は次のようになります。

この増減表から, 図1のようなグラフを想像するかもしれませんが, 実際は, 図2のようなグラフになります。
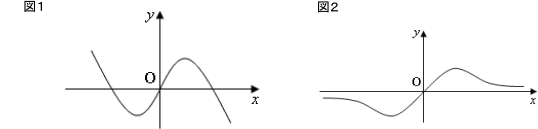
図1のようなグラフだと考えてしまう原因は, x→∞, x→-∞ の状態を調べていないことにあります。
そこで, x→∞, x→-∞ のときの極限を考えると,
"
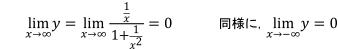
となり, x→∞, x→-∞ のとき, yは0に限りなく近づく, すなわち, x軸が漸近線であることがわかるので, 図2のようなグラフになることがわかります。
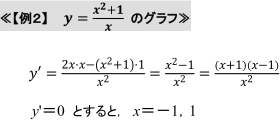
これより, yの増減表を次のようにすると…


この関数の定義域はx≠0であるから, まず増減表のxの段はこのことを踏まえて書かなければなりません。すると, 正しい増減表は次のようになります。

次に, x=0付近の状態を, 右側極限と左側極限を調べて確認しておきます。

◎まとめ
最大値や最小値を求めるとき, グラフを正しくかくためには, 増減の様子や極値を調べる以外に,

を行うとよいでしょう。
もっと正確なグラフをかくことを要求された場合は, これに加えて, 変曲点や漸近線, グラフの対称性などを調べることで, より正確なグラフをかくことができます。
【アドバイス】
グラフは, 最大値・最小値を求める問題や方程式の実数解に関する問題などいろいろな問題で利用します。また, 入試などでも「グラフをかけ。」という問題が出題されているので, 上のまとめにあるポイントを押さえて, どのようなグラフでもかけるように, 練習しておきましょう。
それでは, これで回答を終わります。
これからも, 『進研ゼミ高校講座』にしっかりと取り組んでいってくださいね。













