【複素数平面】絶対値を含む等式の表す図形
両辺を2乗した式の変形の途中で,なぜ両辺に4を加えるのですか?
進研ゼミからの回答
こんにちは。
進研ゼミの教材を利用して頑張っていますね。
いただいた質問について、早速回答させていただきます。
【質問内容】
【問題】
等式|z+2|=2|z-1|を満たす点z全体の描く図形を求めよ。
【解答解説】から抜粋

解答の★の部分で、
なぜ両辺に4を加えるのかわかりません。
というご質問ですね。
【質問への回答】
等式|z+2|=2|z-1|の両辺を2乗して整理すると、
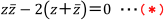
が得られるところまではいいですね。
次に、(*)の両辺に4を加えていますが、これは、この左辺を変形して、円を表す式|z-a|= r の形をつくるための操作なのです。(*)の式の段階で「4を加える」ということはわからなくても気にしなくて大丈夫ですよ。では、どこでわかるかを見ていきましょう。
具体的に(*)式を順に式変形していくと、
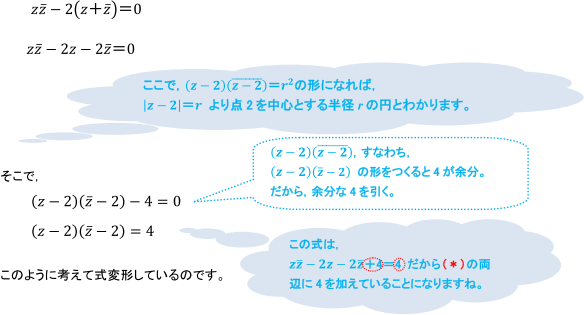
【学習アドバイス】
式変形をするときは、式変形した結果がどのような形になればよいのかを考えながら変形していきましょう。
本問では、円を表す|z-a|=rの形になればよいということを念頭に置きながら式変形すればよいですね。
では、これからも『進研ゼミ高校講座』にしっかりと取り組んでいってくださいね。













